Question

Name the quadrilaterals whose diagonals are equal.
Square; rectangle.
A. True
B. False

Answer 1

Hint – In this question use the property of rectangle as well as square that its adjacent sides are perpendicular to each other later on use the property of Pythagoras theorem so use these concepts to reach the solution of the question.

Complete Step-by-Step solution:

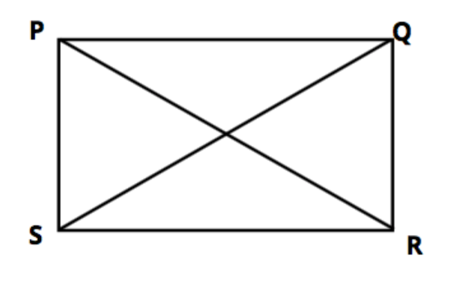
Let suppose we have a rectangle PQRS as shown in the figure.
It’s diagonals are shown as PR and QS, and it divides the rectangle PQRS into 4 triangles which are $\vartriangle PQR,{\text{ }}\vartriangle {\text{PSR, }}\vartriangle {\text{PQS and }}\vartriangle {\text{RQS}}$.
Now the rectangle has a property that each interior angle in it is equal to ${90^0}$.
Thus we can that $\angle PQR = \angle QRS = \angle RSP = \angle SPQ = {90^0}$
Hence $\vartriangle PQR{\text{ and }}\vartriangle {\text{QRS}}$ are right angle triangles.
Using the Pythagoras theorem which is $hypotenus{e^2} = {\text{perpendicula}}{{\text{r}}^2} + bas{e^2}$ in $\vartriangle PQR $ we get
${\text{P}}{{\text{R}}^2} = P{Q^2} + R{Q^2}$……………… (1)
Using Pythagoras theorem in $\vartriangle {\text{QRS}}$ we get,
${\text{Q}}{{\text{S}}^2} = S{R^2} + R{Q^2}$…………………. (2)
A rectangle has opposite sides equal thus PQ=SR and SP=RQ
Using PQ=SR in equation (1) and (2) we get
${\text{P}}{{\text{R}}^2} = P{Q^2} + R{Q^2}$And ${\text{Q}}{{\text{S}}^2} = P{Q^2} + R{Q^2}$
Thus
$
   \Rightarrow P{R^2} = Q{S^2} \\
   \Rightarrow PR = QS \\
$
Clearly PR and QS are the diagonals of the rectangle PQRS, hence the rectangle is a quadrilateral whose diagonals are equal is true.
The definition of square is, it is a special type of rectangle only however in it all the sides are equal. Thus all the properties of the rectangle will be applicable to a square, hence we can say that square is a quadrilateral whose diagonals are equal.
Hence option (A) is the right answer.

Note – Whenever we face such types of questions the key concept is Pythagoras theorem as we know Pythagoras theorem is only applicable to right angle triangles, as we know that the adjacent sides of square and rectangle perpendicular to each other so we easily apply the Pythagoras theorem so apply Pythagoras theorem in triangle PQR and QRS then apply the property that in a rectangle opposite sides are equal so use this property as above and simplify we can see that the two diagonals are equal, similarly in square all sides are equal remaining concept is same hence the two diagonals are equal which is the required answer.