Question

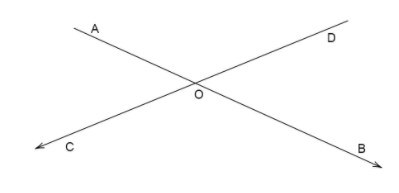
Name the four pairs of supplementary angles shown in the figure.

Answer 1

Hint:From the knowledge of supplementary angles that they are the angles which lie on a straight line and sum up to \[{180^ \circ }\], we name the pairs( set of two angles ) which are supplementary in nature.

Complete step-by-step answer:
We know the two lines \[AB,CD\] intersect at point \[O\].
A pair of supplementary angles will be formed if on straight line is cut by another straight line at a point.
So the supplementary angles will be formed at the point of intersection of two lines \[AB,CD\].
We take the line \[AB\] which is cut by the line \[CD\].
This divides the area into four parts and the angles formed around the point of intersection are four angles in total.
Since we know angles on a straight line sum up to be \[{180^ \circ }\]
\[\angle AOB + \angle BOD = {180^ \circ }\] and \[\angle AOC + \angle BOC = {180^ \circ }\]
Therefore set of angles seen from above on a straight line \[AB\] are \[\angle AOB,\angle BOD\]
And the set of angles seen from below on a straight line \[AB\] are \[\angle AOC,\angle BOC\]
Similarly if we take the line \[CD\] which is cut by the line \[AB\].
This divides the area into four parts and the angles formed around the point of intersection are four angles in total.
Since we know angles on a straight line sum up to be \[{180^ \circ }\]
\[\angle COA + \angle DOA = {180^ \circ }\] and \[\angle COB + \angle DOB = {180^ \circ }\]
Therefore set of angles seen from above on a straight line \[CD\] are \[\angle COA,\angle DOA\]
And the set of angles seen from below on a straight line \[CD\] are \[\angle COB,\angle DOB\]
Therefore, four pair of supplementary angles in the given figure are
* \[\angle AOB,\angle BOD\]
*\[\angle AOC,\angle BOC\]
* \[\angle COA,\angle DOA\]
*\[\angle COB,\angle DOB\]

Note:Students are likely to make the mistake of collecting all the possible pairs formed in this diagram which is wrong because there are also vertically opposite angles in the diagram which are not supplementary to each other.