Question

Name the angles in the given figure

Answer 1

Hint: We use the definition of angles and the fact that an angle is formed at the point or vertex where two line segments or two rays meet. Calculate total number of vertices and write angle for each of the vertices.
* An angle is always formed at the vertex of a figure where two line segments meet each other or where two rays meet each other. It is denoted by the three alphabets taken in order such that the vertex where angle is formed comes in center.
* A polygon is a closed simple figure which is made of only line segments.

Complete answer:
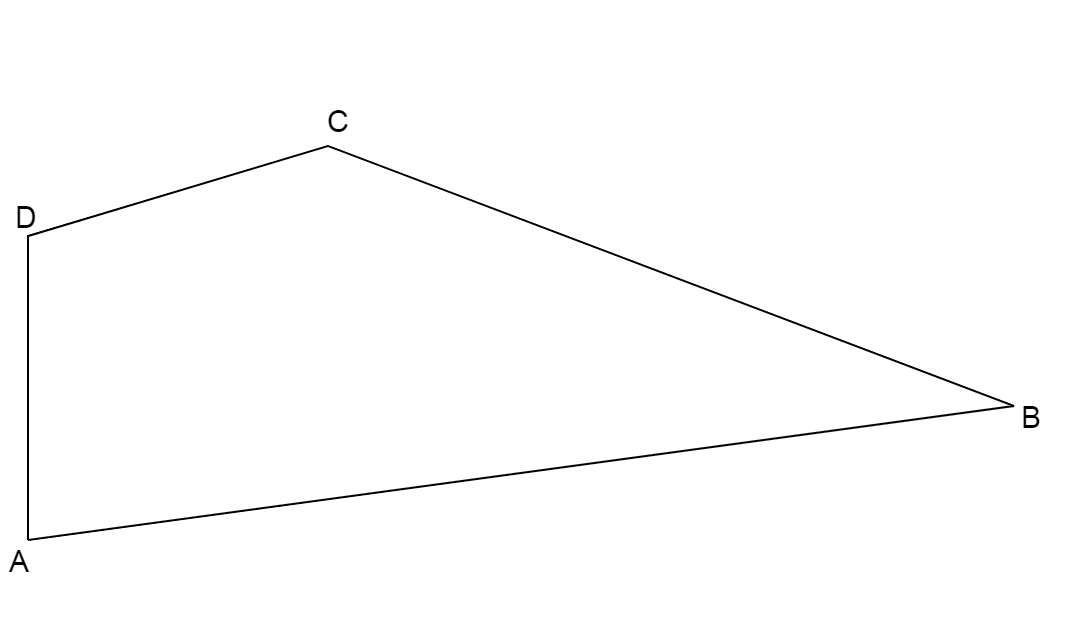
We are given a polygon ABCD.
Here we have four vertices of the polygon A, B, C and D
We know an angle is made where two line segments meet. Here the sides of the polygon are the line segments.
Sides of polygon are AB, BC, CD and DA
We write the vertex where two line segments meet and write the angle associated with that vertex.
1) AB and BC:
Since AB and BC are sides of the polygon ABCD and they meet at the vertex B; the angle will be formed at vertex B.
Angle formed at vertex B is \[\angle ABC\] … (1)
2) BC and CD:
Since BC and CD are sides of the polygon ABCD and they meet at the vertex C; the angle will be formed at vertex C.
Angle formed at vertex C is \[\angle BCD\] … (2)
3) CD and DA:
Since CD and DA are sides of the polygon ABCD and they meet at the vertex D; the angle will be formed at vertex D.
Angle formed at vertex D is \[\angle CDA\] … (3)
4) DA and AB:
Since DA and AB are sides of the polygon ABCD and they meet at the vertex A; the angle will be formed at vertex A.
Angle formed at vertex A is \[\angle DAB\] … (4)
From equations (1), (2), (3) and (4) we write the names of angles in the figure as \[\angle ABC,\angle BCD,\angle CDA,\angle DAB\]

\[\therefore \]Angles formed in the figure are \[\angle ABC,\angle BCD,\angle CDA,\angle DAB\]

Note:
Many students make mistake of writing the angles by only using the vertex at which the angle is formed i.e. like \[\angle A,\angle B,\angle C,\angle D\], keep in mind we avoid using this way of representation as in many cases there are more than one angles formed at the vertex. Also it is always recommended to write a three letter angle name as it depicts the path from where to where we are taking the angle.