Question

When $n$ is small (less than $30$ ), how does the shape of the $t$ distribution compare to the normal distribution?

Answer 1

Hint: Here in this question we have been asked to compare the shape of the $t$ distribution with that of the normal distribution, when $n$ is small (less than $30$ ). We know that $t$ distribution is a type of probability distribution that is similar to the normal distribution and it has a greater chance for extreme values than normal distribution.

Complete step-by-step answer:
Now considering from the question we have been asked to compare the shape of the $t$ distribution with that of the normal distribution, when $n$ is small (less than $30$ ).
We know that $t$ distribution is a type of probability distribution that is similar to the normal distribution and it has a greater chance for extreme values than normal distribution.
Here a diagram is shown for $t$ distributions of different degrees and normal distribution in a single plot so that we can compare them easily. Observe them carefully and draw the required conclusions.

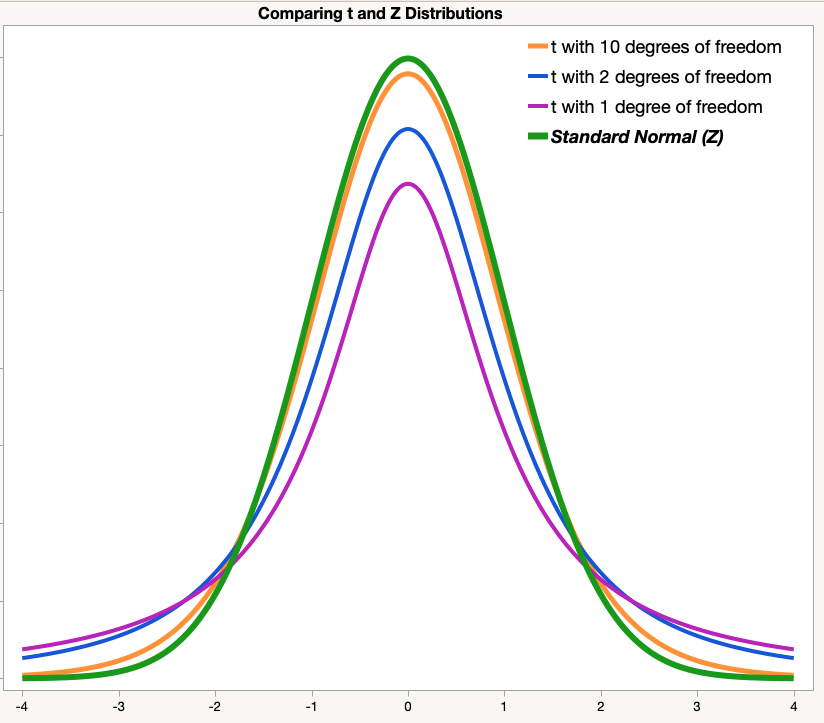
Hence we can conclude that when $n$ is small (less than $30$ ), the shape of the $t$ distribution will be flatter and more spread out when compared to the normal distribution.

Note: In questions of this type we should be sure with the concepts that we are applying in between the steps during the process of answering. This is a pure concept based question and it is clearly derived from the concepts of statistics.