
What must be subtracted to \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] so that the result is exactly divisible by ${x^2} + x - 2$ ?
Answer
589.2k+ views
Hint:If $p\left( x \right)$ and $g\left( x \right)$ are two polynomials such that degree of $p\left( x \right) \geqslant $ degree of $g\left( x \right)$ and $g\left( x \right) \ne 0$ , then we have polynomials $q\left( x \right)$ and $r\left( x \right)$ such that:
$p\left( x \right) = \;g\left( x \right)q\left( x \right) + r\left( x \right)$
Where $r\left( x \right) = 0$ or degree of $r\left( x \right) < $ degree of $g\left( x \right)$. Here $p\left( x \right)$ is divided by $g\left( x \right)$, gives $q\left( x \right)$ as quotient and $r\left( x \right)$ as remainder.
The process of division continues until the remainder is 0 or the degree of the new dividend is less than the degrees of the divisor. At this stage, the new dividend becomes the remainder and the sum of the quotients gives us the whole quotient.
If the remainder is not 0, that means the dividend is not exactly divisible by divisor. To make the dividend exactly divisible by the divisor, the remainder should be subtracted from the dividend. Let us understand this by taking an example:
Complete step-by-step answer:
Write dividends and divisors in the standard form.
i.e. arranging the terms in descending order of their degrees.
In the given question they are already in standard form so that dividend is \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] and the divisor is ${x^2} + x - 2$.
Write the first term of the quotient
We divide the first term of the dividend by the first term of the divisor, i.e. we divide \[{x^4}\] by ${x^2}$ and get ${x^2}$ . This gives the first term of the quotient.
$\dfrac{{{x^4}}}{{{x^2}}} = {x^2}$ (first term of the quotient)
Multiply divisor by the first term of the quotient.
We multiply the divisor by the first term of the quotient and subtract the product from the dividend, i.e. we multiply ${x^2} + x - 2$ by ${x^2}$ and subtract the product ${x^4} + {x^3} - 2\;{x^2}$ from the dividend \[{x^4} + 2{x^3} - 2{x^2} + x - 1\]. This gives the remainder as ${x^3} + x - 1$
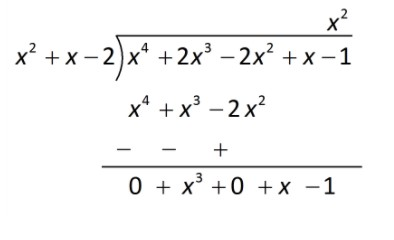
Write the second term of the quotient.
We treat the remainder as the new dividend. The divisor remains the same. We repeat step 2 to get the next term of the quotient, i.e., we divide the first term ${x^3}$ of the (new) dividend by the first term ${x^2}$ of the divisor and obtain $x$. Thus $x$is the second term of the quotient.
\[\dfrac{{{x^3}}}{{{x^2}}} = x\] (second term of the quotient)
${x^2} + x$ (new quotient)
Multiply divisor by the second term of the quotient.
We multiply the divisor by the second term of the quotient and subtract the product from the dividend, i.e. we multiply ${x^2} + x - 2$ by $x$ and subtract the product ${x^3} + {x^2} - 2\;x$ from the dividend ${x^3} + x - 1$ . This gives the remainder as $ - {x^2} + 3x - 1$
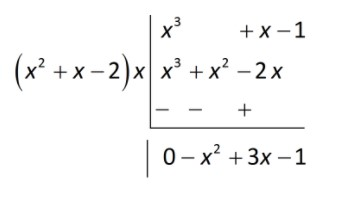
Write the third term of the quotient.
We treat the remainder as the new dividend. The divisor remains the same. We repeat step 2 to get the next term of the quotient, i.e., we divide the first term $ - {x^2}$ of the (new) dividend by the first term ${x^2}$ of the divisor and obtain -1. Thus -1 is the third term of the quotient.
\[\dfrac{{ - {x^2}}}{{{x^2}}} = - 1\] (third term of the quotient)
${x^2} + x - 1$ (new quotient)
Multiply divisor by the third term of the quotient.
We multiply the divisor by the third term of the quotient and subtract the product from the dividend, i.e. we multiply ${x^2} + x - 2$ by -1 and subtract the product $ - {x^2} - x + 2$ from the dividend $ - {x^2} + 3x - 1$ . This gives the remainder as $4x - 3$.
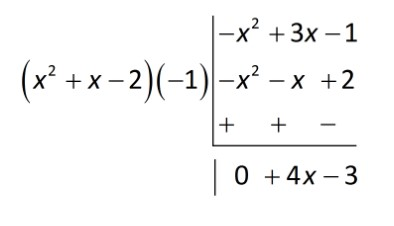
The degree of the remainder $4x - 3$ is less than the degree of the divisor ${x^2} + x - 2$, thus the quotient is ${x^2} + x - 1$ and the remainder is $4x - 3$ .
The whole division.
Let’s see the whole division process done above as a whole.
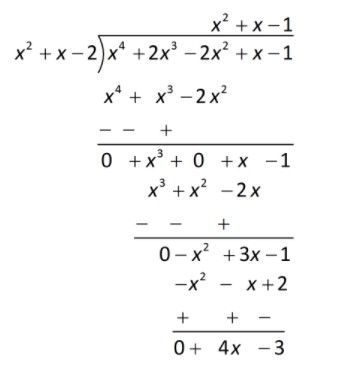
Make the dividend exactly divisible by divisor.
The remainder obtained $\left( {4x - 3} \right) \ne 0$ , that means \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] is not exactly divisible by ${x^2} + x - 2$ .
Thus, subtract $4x - 3$ from \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] for the polynomial to be exactly divisible by ${x^2} + x - 2$ .
Hence, \[{x^4} + 2{x^3} - 2{x^2} + x - 1 - \left( {4x - 3} \right)\]
\[ \Rightarrow {x^4} + 2{x^3} - 2{x^2} + x - 1 - 4x + 3\]
\[ \Rightarrow {x^4} + 2{x^3} - 2{x^2} - 3x + 2\] is exactly divisible by ${x^2} + x - 2$ .
So, $4x - 3$ should be subtracted to \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] so that the result is exactly divisible by ${x^2} + x - 2$ .
Note:Similarly, the addition of $\left[ {{x^2} + x - 2 - \left( {4x - 3} \right)} \right]$ i.e. ${x^2} - 3x + 1$ to the polynomial \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] will also make the polynomial exactly divisible by ${x^2} + x - 2$ .
I.e., \[{x^4} + 2{x^3} - 2{x^2} + x - 1 + {x^2} - 3x + 1\] \[ \Rightarrow {x^4} + 2{x^3} - {x^2} - 2x\] is exactly divisible by ${x^2} + x - 2$ .
$p\left( x \right) = \;g\left( x \right)q\left( x \right) + r\left( x \right)$
Where $r\left( x \right) = 0$ or degree of $r\left( x \right) < $ degree of $g\left( x \right)$. Here $p\left( x \right)$ is divided by $g\left( x \right)$, gives $q\left( x \right)$ as quotient and $r\left( x \right)$ as remainder.
The process of division continues until the remainder is 0 or the degree of the new dividend is less than the degrees of the divisor. At this stage, the new dividend becomes the remainder and the sum of the quotients gives us the whole quotient.
If the remainder is not 0, that means the dividend is not exactly divisible by divisor. To make the dividend exactly divisible by the divisor, the remainder should be subtracted from the dividend. Let us understand this by taking an example:
Complete step-by-step answer:
Write dividends and divisors in the standard form.
i.e. arranging the terms in descending order of their degrees.
In the given question they are already in standard form so that dividend is \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] and the divisor is ${x^2} + x - 2$.
Write the first term of the quotient
We divide the first term of the dividend by the first term of the divisor, i.e. we divide \[{x^4}\] by ${x^2}$ and get ${x^2}$ . This gives the first term of the quotient.
$\dfrac{{{x^4}}}{{{x^2}}} = {x^2}$ (first term of the quotient)
Multiply divisor by the first term of the quotient.
We multiply the divisor by the first term of the quotient and subtract the product from the dividend, i.e. we multiply ${x^2} + x - 2$ by ${x^2}$ and subtract the product ${x^4} + {x^3} - 2\;{x^2}$ from the dividend \[{x^4} + 2{x^3} - 2{x^2} + x - 1\]. This gives the remainder as ${x^3} + x - 1$
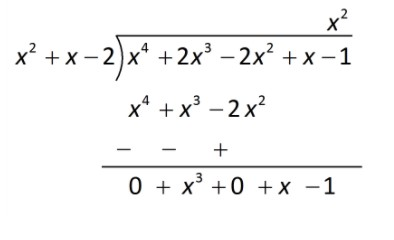
Write the second term of the quotient.
We treat the remainder as the new dividend. The divisor remains the same. We repeat step 2 to get the next term of the quotient, i.e., we divide the first term ${x^3}$ of the (new) dividend by the first term ${x^2}$ of the divisor and obtain $x$. Thus $x$is the second term of the quotient.
\[\dfrac{{{x^3}}}{{{x^2}}} = x\] (second term of the quotient)
${x^2} + x$ (new quotient)
Multiply divisor by the second term of the quotient.
We multiply the divisor by the second term of the quotient and subtract the product from the dividend, i.e. we multiply ${x^2} + x - 2$ by $x$ and subtract the product ${x^3} + {x^2} - 2\;x$ from the dividend ${x^3} + x - 1$ . This gives the remainder as $ - {x^2} + 3x - 1$
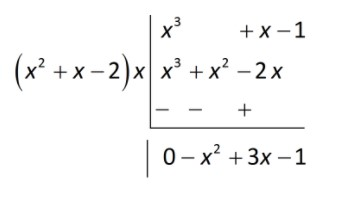
Write the third term of the quotient.
We treat the remainder as the new dividend. The divisor remains the same. We repeat step 2 to get the next term of the quotient, i.e., we divide the first term $ - {x^2}$ of the (new) dividend by the first term ${x^2}$ of the divisor and obtain -1. Thus -1 is the third term of the quotient.
\[\dfrac{{ - {x^2}}}{{{x^2}}} = - 1\] (third term of the quotient)
${x^2} + x - 1$ (new quotient)
Multiply divisor by the third term of the quotient.
We multiply the divisor by the third term of the quotient and subtract the product from the dividend, i.e. we multiply ${x^2} + x - 2$ by -1 and subtract the product $ - {x^2} - x + 2$ from the dividend $ - {x^2} + 3x - 1$ . This gives the remainder as $4x - 3$.
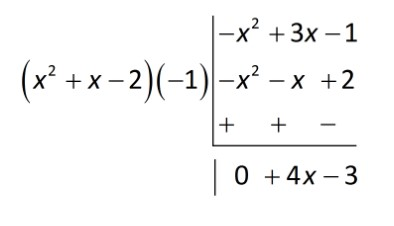
The degree of the remainder $4x - 3$ is less than the degree of the divisor ${x^2} + x - 2$, thus the quotient is ${x^2} + x - 1$ and the remainder is $4x - 3$ .
The whole division.
Let’s see the whole division process done above as a whole.
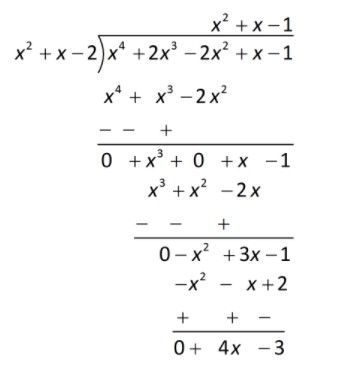
Make the dividend exactly divisible by divisor.
The remainder obtained $\left( {4x - 3} \right) \ne 0$ , that means \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] is not exactly divisible by ${x^2} + x - 2$ .
Thus, subtract $4x - 3$ from \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] for the polynomial to be exactly divisible by ${x^2} + x - 2$ .
Hence, \[{x^4} + 2{x^3} - 2{x^2} + x - 1 - \left( {4x - 3} \right)\]
\[ \Rightarrow {x^4} + 2{x^3} - 2{x^2} + x - 1 - 4x + 3\]
\[ \Rightarrow {x^4} + 2{x^3} - 2{x^2} - 3x + 2\] is exactly divisible by ${x^2} + x - 2$ .
So, $4x - 3$ should be subtracted to \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] so that the result is exactly divisible by ${x^2} + x - 2$ .
Note:Similarly, the addition of $\left[ {{x^2} + x - 2 - \left( {4x - 3} \right)} \right]$ i.e. ${x^2} - 3x + 1$ to the polynomial \[{x^4} + 2{x^3} - 2{x^2} + x - 1\] will also make the polynomial exactly divisible by ${x^2} + x - 2$ .
I.e., \[{x^4} + 2{x^3} - 2{x^2} + x - 1 + {x^2} - 3x + 1\] \[ \Rightarrow {x^4} + 2{x^3} - {x^2} - 2x\] is exactly divisible by ${x^2} + x - 2$ .
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




