
What must be subtracted from $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ so that the resulting polynomial is exactly divisible ${{x}^{2}}-3x+2$?
[a] x-1
[b] 200x+200
[c] 219x-200
[d] -219x+200
Answer
586.2k+ views
Hint:Use the fact that the remainder obtained on dividing p(x) by x-a is given by $p\left( a \right)$. Hence prove that $\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-1}=g\left( x \right)+\dfrac{19}{x-1}$, where g(x) is some polynomial and $\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-2}=h\left( x \right)+\dfrac{238}{x-2}$
Use the fact that $\dfrac{1}{{{x}^{2}}-3x+2}=\dfrac{1}{\left( x-2 \right)\left( x-1 \right)}=\dfrac{1}{x-2}-\dfrac{1}{x-1}$
Hence prove that
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{\left( {{x}^{2}}-3x+2 \right)}=h\left( x \right)-g\left( x \right)+\left( \dfrac{238}{x-2}-\dfrac{19}{x-1} \right)$
Hence find the remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by ${{x}^{2}}-3x+2$. Hence find the polynomial that should be subtracted from $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ so that the resulting polynomial is divisible by ${{x}^{2}}-3x+2$
Complete step by step answer:
Let r be remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by $x-1$
Hence, we have
$8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=g\left( x \right)\left( x-1 \right)+r$ where g(x) is some polynomial.
Put x = 1, we get
$\begin{align}
& 8+14-2+7-8=g\left( 1 \right)\left( 1-1 \right)+r \\
& \Rightarrow r=19 \\
\end{align}$
Hence, we have $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=g\left( x \right)\left( x-1 \right)+19$
Dividing both sides by x-1, we get
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-1}=g\left( x \right)+\dfrac{19}{x-1}\text{ }\left( i \right)$
Let s be the remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by x-2.
Hence, we have
$8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=h\left( x \right)\left( x-2 \right)+s$, where h(x) is some polynomial.
Put x= 2, we get
$\begin{align}
& 8\times {{2}^{4}}+14\times {{2}^{3}}-2\times {{2}^{2}}+7\times 2-8=h\left( 2 \right)\left( 2-2 \right)+s \\
& \Rightarrow s=238 \\
\end{align}$
Hence, we have
$8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=h\left( x \right)\left( x-2 \right)+238$
Divide both sides by $x-2$, we get
\[\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-2}=h\left( x \right)+\dfrac{238}{x-2}\text{ }\left( ii \right)\]
Now, we have ${{x}^{2}}-3x+2={{x}^{2}}-2x-x+2$
Taking x common from the first two terms and -1 common from the last two terms, we get
${{x}^{2}}-3x+2=x\left( x-2 \right)-1\left( x-2 \right)$
Take x-2 common, we get
${{x}^{2}}-3x+2=\left( x-2 \right)\left( x-1 \right)$
Hence, we have
$\dfrac{1}{{{x}^{2}}-3x+2}=\dfrac{1}{\left( x-1 \right)\left( x-2 \right)}=\dfrac{x-1-\left( x-2 \right)}{\left( x-1 \right)\left( x-2 \right)}=\dfrac{1}{x-2}-\dfrac{1}{x-1}$
Hence, we have
\[\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{\left( x-1 \right)\left( x-2 \right)}=\left( 8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8 \right)\left( \dfrac{1}{x-2}-\dfrac{1}{x-1} \right)\]
Hence by distributive property of multiplication over addition, we have
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-2}-\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-1}$
From equation (i) and equation (ii), we get
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=h\left( x \right)+\dfrac{238}{x-2}-g\left( x \right)-\dfrac{19}{x-1}$
Hence, we have
$\begin{align}
& \dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=h\left( x \right)-g\left( x \right)+\dfrac{1}{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}\left( 238x-238-19x+38 \right) \\
& =h\left( x \right)-g\left( x \right)+\dfrac{1}{{{x}^{2}}-3x+2}\left( 219x-200 \right) \\
\end{align}$
Hence the remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by ${{x}^{2}}-3x+2$ is $219x-200$
Hence the polynomial that must be subtracted from $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ to make it divisible by ${{x}^{2}}-3x+2$ us $219x-200$
Hence option [c] is correct
Note:
Verification: We can verify the correctness of our solution by checking that $219x-200$ subtracted from $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ is divisible by ${{x}^{2}}-3x+2$
We have $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8-219x+200=8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}-212x+192$
Now, we have
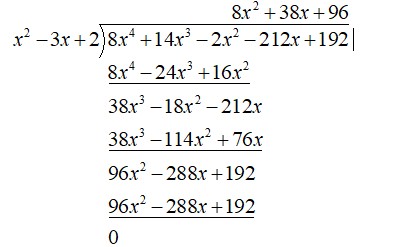
Hence our solution is verified to be correct.
Use the fact that $\dfrac{1}{{{x}^{2}}-3x+2}=\dfrac{1}{\left( x-2 \right)\left( x-1 \right)}=\dfrac{1}{x-2}-\dfrac{1}{x-1}$
Hence prove that
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{\left( {{x}^{2}}-3x+2 \right)}=h\left( x \right)-g\left( x \right)+\left( \dfrac{238}{x-2}-\dfrac{19}{x-1} \right)$
Hence find the remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by ${{x}^{2}}-3x+2$. Hence find the polynomial that should be subtracted from $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ so that the resulting polynomial is divisible by ${{x}^{2}}-3x+2$
Complete step by step answer:
Let r be remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by $x-1$
Hence, we have
$8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=g\left( x \right)\left( x-1 \right)+r$ where g(x) is some polynomial.
Put x = 1, we get
$\begin{align}
& 8+14-2+7-8=g\left( 1 \right)\left( 1-1 \right)+r \\
& \Rightarrow r=19 \\
\end{align}$
Hence, we have $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=g\left( x \right)\left( x-1 \right)+19$
Dividing both sides by x-1, we get
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-1}=g\left( x \right)+\dfrac{19}{x-1}\text{ }\left( i \right)$
Let s be the remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by x-2.
Hence, we have
$8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=h\left( x \right)\left( x-2 \right)+s$, where h(x) is some polynomial.
Put x= 2, we get
$\begin{align}
& 8\times {{2}^{4}}+14\times {{2}^{3}}-2\times {{2}^{2}}+7\times 2-8=h\left( 2 \right)\left( 2-2 \right)+s \\
& \Rightarrow s=238 \\
\end{align}$
Hence, we have
$8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8=h\left( x \right)\left( x-2 \right)+238$
Divide both sides by $x-2$, we get
\[\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-2}=h\left( x \right)+\dfrac{238}{x-2}\text{ }\left( ii \right)\]
Now, we have ${{x}^{2}}-3x+2={{x}^{2}}-2x-x+2$
Taking x common from the first two terms and -1 common from the last two terms, we get
${{x}^{2}}-3x+2=x\left( x-2 \right)-1\left( x-2 \right)$
Take x-2 common, we get
${{x}^{2}}-3x+2=\left( x-2 \right)\left( x-1 \right)$
Hence, we have
$\dfrac{1}{{{x}^{2}}-3x+2}=\dfrac{1}{\left( x-1 \right)\left( x-2 \right)}=\dfrac{x-1-\left( x-2 \right)}{\left( x-1 \right)\left( x-2 \right)}=\dfrac{1}{x-2}-\dfrac{1}{x-1}$
Hence, we have
\[\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{\left( x-1 \right)\left( x-2 \right)}=\left( 8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8 \right)\left( \dfrac{1}{x-2}-\dfrac{1}{x-1} \right)\]
Hence by distributive property of multiplication over addition, we have
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-2}-\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{x-1}$
From equation (i) and equation (ii), we get
$\dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=h\left( x \right)+\dfrac{238}{x-2}-g\left( x \right)-\dfrac{19}{x-1}$
Hence, we have
$\begin{align}
& \dfrac{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}{{{x}^{2}}-3x+2}=h\left( x \right)-g\left( x \right)+\dfrac{1}{8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8}\left( 238x-238-19x+38 \right) \\
& =h\left( x \right)-g\left( x \right)+\dfrac{1}{{{x}^{2}}-3x+2}\left( 219x-200 \right) \\
\end{align}$
Hence the remainder obtained on dividing $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ by ${{x}^{2}}-3x+2$ is $219x-200$
Hence the polynomial that must be subtracted from $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ to make it divisible by ${{x}^{2}}-3x+2$ us $219x-200$
Hence option [c] is correct
Note:
Verification: We can verify the correctness of our solution by checking that $219x-200$ subtracted from $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8$ is divisible by ${{x}^{2}}-3x+2$
We have $8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+7x-8-219x+200=8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}-212x+192$
Now, we have
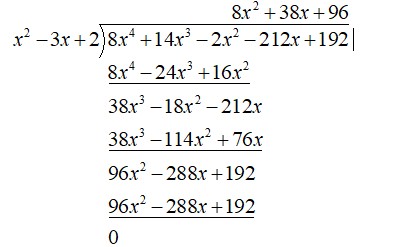
Hence our solution is verified to be correct.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Who gave "Inqilab Zindabad" slogan?

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE




