Question

Multiply \[405 \times 367\] using the Lattice method.

Answer 1

Hint: We use the concept of the lattice method and write the digits of both the numbers on adjacent sides of the 3 by 3 square. The method is explained as step-by-step as:
1) Each digit of the first number is placed on the head of the columns and each digit of the second number is placed on the end of the rows.
2) Multiply each value on top of the column by each value on the right side of the row one by one and write the values in their corresponding places.
3) Each box in 3 by 3 box is cut by a diagonal line such that the tens element of multiplied number lies above the line and the ones element of the multiplied number lies below the line.

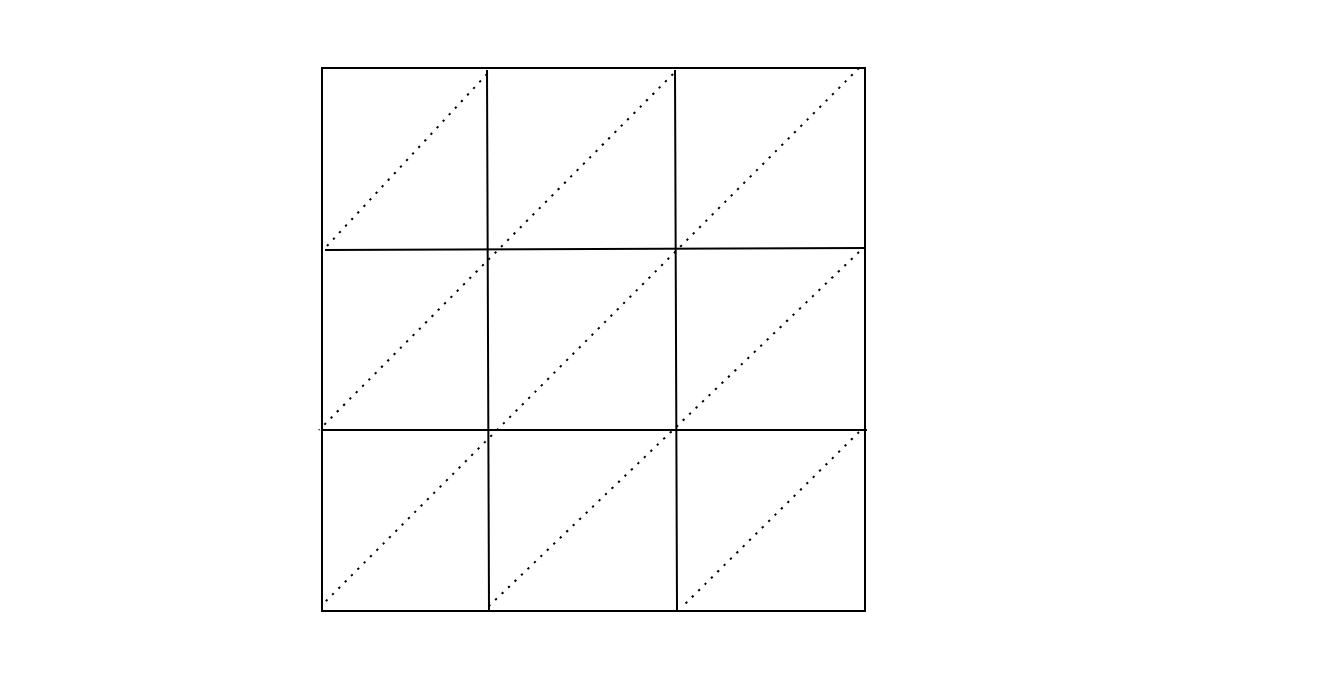
4) Sum elements between the diagonals starting from the bottom right side and move upwards in the same way. Sum having digit in tens place is written as only the one’s element and the tens element is carried to the diagonal above it. Write respective sums on the left side of the rows and below the columns.

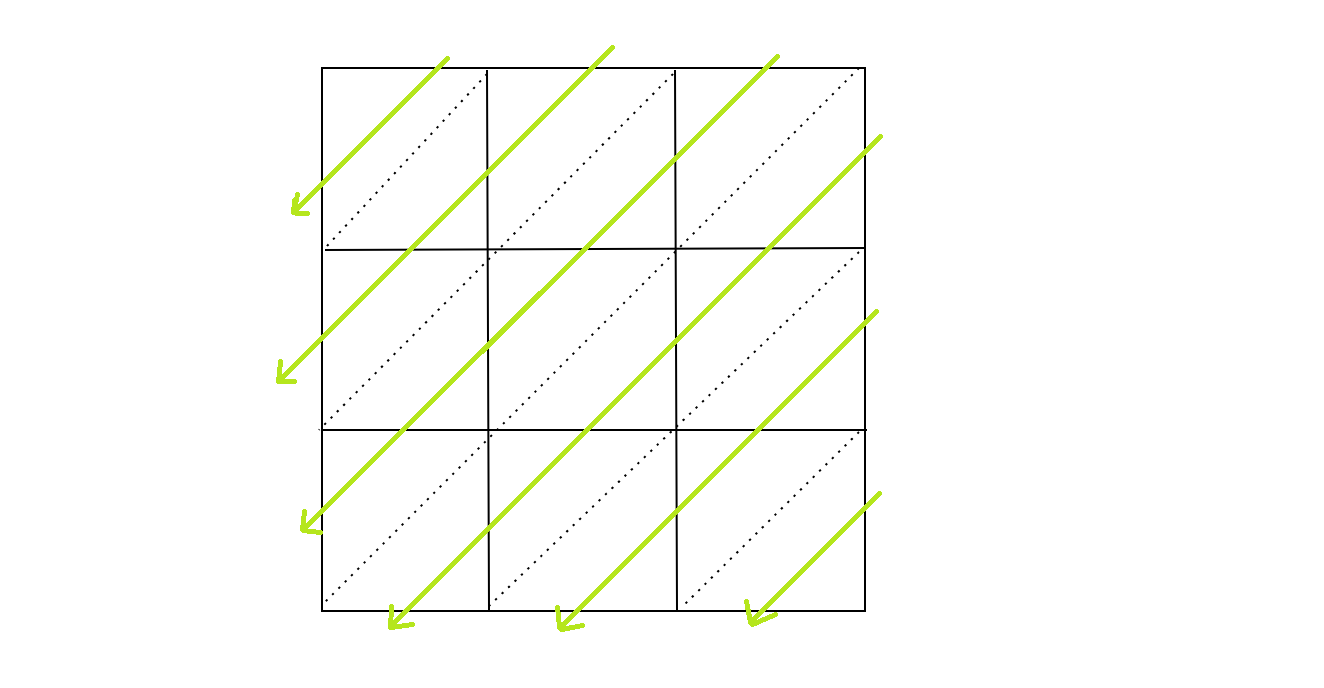
5) Write the product of two numbers as the number formed on the L shape of the box.

Complete step by step answer:
We have to find the product of \[405 \times 367\]
Here the first number is 405 and the second number is 367.
We draw a \[3 \times 3\] square which has \[3 \times 3 = 9\] blocks in it.
Write each digit of the first number ($405$) on the top of each column. Also, write each digit of the second number ($367$) at the end of each row.

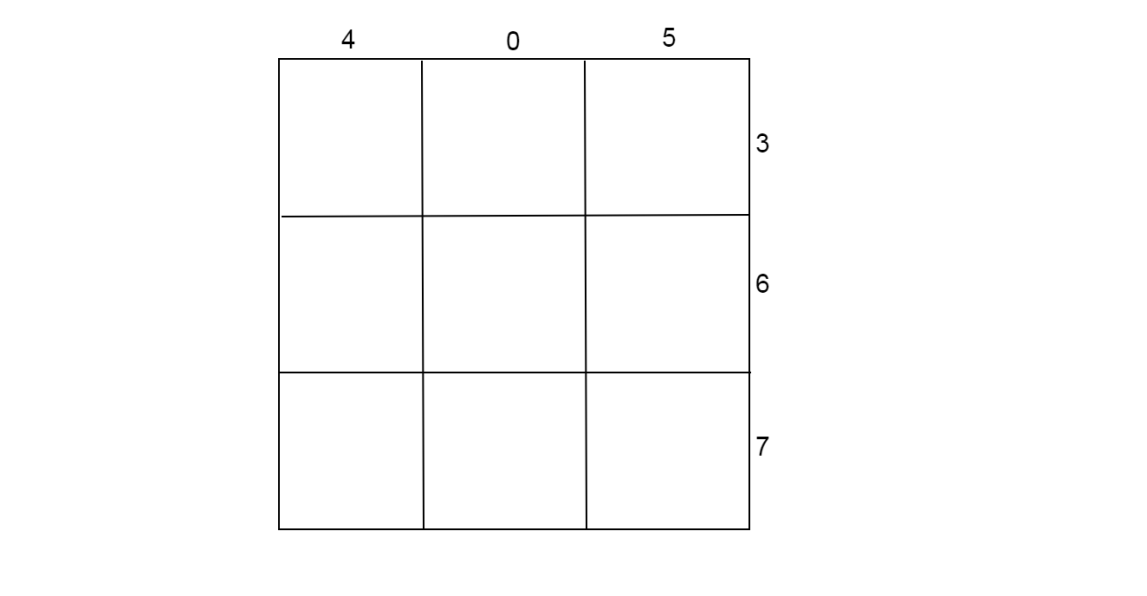
Write the product of each element on top of each column with each element on the right side of each row in the respective blocks. Write the tens element above the diagonal and one element below the diagonal.

Draw diagonals within each block. Write the tens element of the respective product above the diagonal and ones element of the respective product below the diagonal.

Add elements within each diagonal starting from the bottom right. Draw arrows to depict the direction in which we are adding the digits. Write the ones element of the sum obtained where the arrow is pointed and carry forward the tens digit to the sum of elements between the diagonals above it.

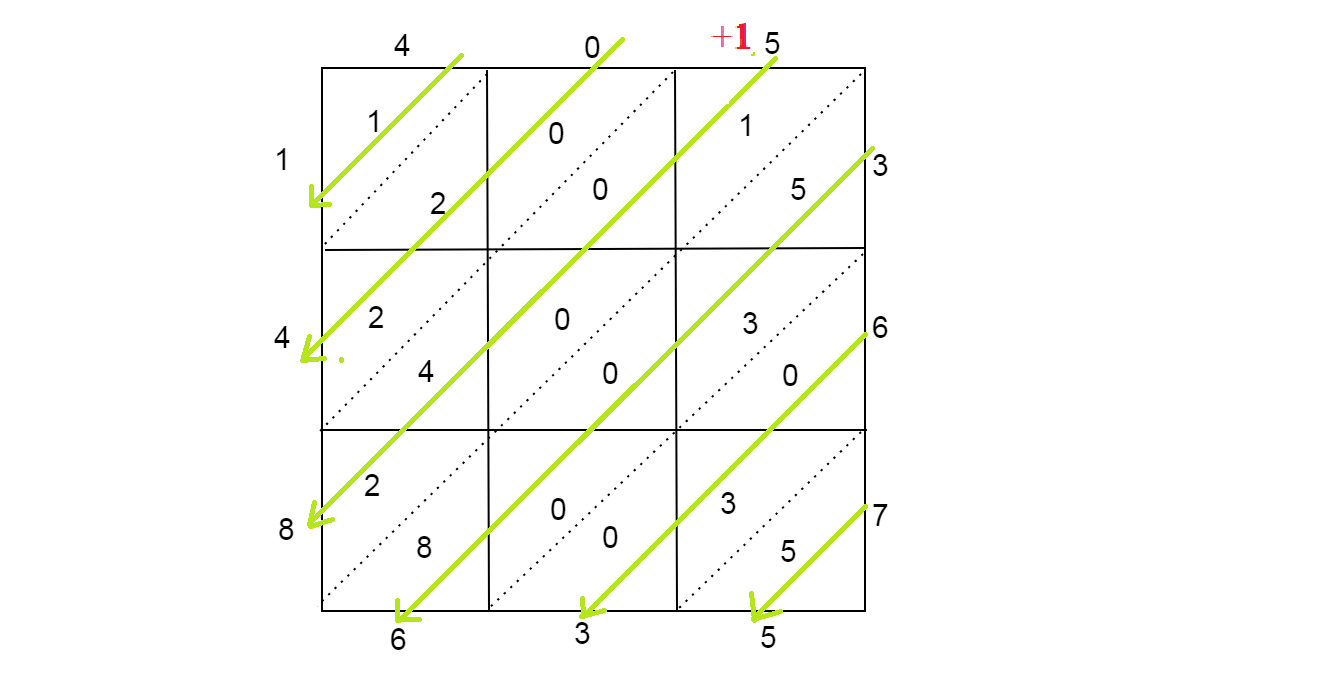
Now we write the product \[405 \times 367\] starting from top left and moving till bottom right in L route.

\[\therefore 405 \times 367 = 148635\]. Thus, the product obtained from lattice method of multiplication is 148635.

Note:
Students many times make mistakes while adding the elements in the diagonal as they start adding from the topmost left diagonal and move down. This is the wrong procedure; we always add the diagonals starting from the bottom. Represent the arrows that show the addition of diagonals with a different color for clear representation.