Question

Multiply \[405 \times 367\] using the lattice method.

Answer 1

Hint: In this question we have to multiply the given terms by using the lattice method. For this first we have to know what the lattice method is.
Lattice Method:
We first calculate a product for each cell by multiplying the digit at the top of the column and the digit at the right of the row. The tens digit of the product is placed above the diagonal that passes through the cell, and the units digit is put below that diagonal.
Multiplication by lattice method:
Write the numbers to be multiplied on the top and on the right.
Multiply the number on the top of the box with the number to the right of the box and write the answer in the box.
Add the numbers in the box diagonally and carry to the next column when necessary.
After the grid is completed, we will get the multiplication.

Complete step-by-step answer:
We need to multiply \[405 \times 367\] using the lattice method.
Arrange \[405\] and \[367\] around a \[3 \times 3\] grid as shown below
               

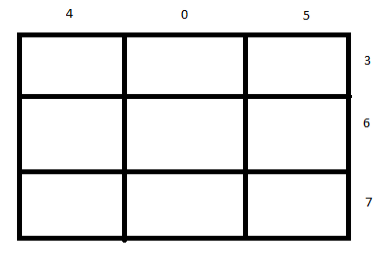
Multiply \[3\] by \[4\] to get \[12\] and put \[12\] in the intersection of the first row and the first column as shown below.

Notice that \[3\] is located in the first row and \[4\] in the first column. That is why the answer goes in the intersection.

By the same token, multiply \[6\] and \[0\], put the answer in the intersection of the second row and the second column and so forth…
               

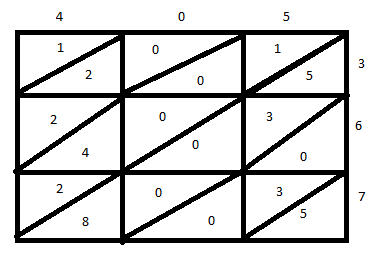
Then, going from right to left, add the numbers down the diagonals.

The first diagonal has only \[5\]. Bring \[5\] down.

The second diagonal has \[0,3,0\]. Adding these numbers we get \[3\]. Bring 3 down.

The third diagonal has \[5, 3, 0, 0\] and \[8\]. Add these numbers we get \[16\]. Bring \[6\] down and carry the \[1\] over to the next diagonal.
The fourth diagonal has \[1, 0, 0, 4, 2\].Add these numbers we get \[7\] and add \[1\] (your carry) to \[7\] to get \[8\].
and so forth...
               

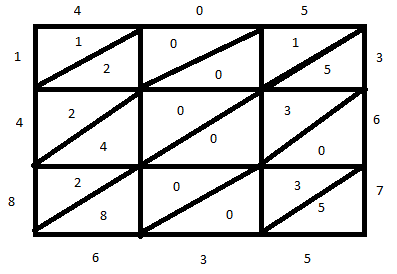
After the grid is completed, what we get is the answer to the multiplication that is \[148635\].

Note: Grids should be made properly. Take care while joining diagonals of squares. Or else our answer may go wrong. This is like our traditional method only. But in a much easier way. As in this method, the steps are broken & carried forward digits are written within the grids. We can be friendly with this method by more & more practice.