
What is the multiplicity of the real root of an equation that crosses/touches the $x$ axis once?
Answer
528.9k+ views
Hint: In this problem we need to check the multiplicity of the real root of an equation which crosses/touches the $x$ axis once. For this we will consider any two equations which touch or cross the $x$ axis once along with the roots of both the assumed equations. By observing the roots and graphs of the assumed equations we can simplify answering the question.
Complete step-by-step solution:
Let us assume the equation $f\left( x \right)={{x}^{3}}$.
The graph of the function $f\left( x \right)={{x}^{3}}$ would be
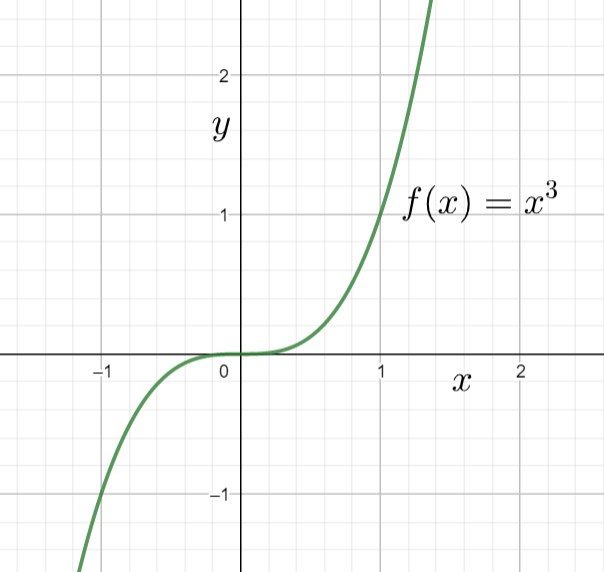
We can observe that the function $f\left( x \right)={{x}^{3}}$ touches the $x$ axis once. The roots of the equation $f\left( x \right)={{x}^{3}}$ are $x=0,0,0$. The multiplicity of the root $0$ is $3$.
Now let us consider the function $g\left( x \right)={{x}^{3}}+x$. The graph of the equation $g\left( x \right)={{x}^{3}}+x$ is given by
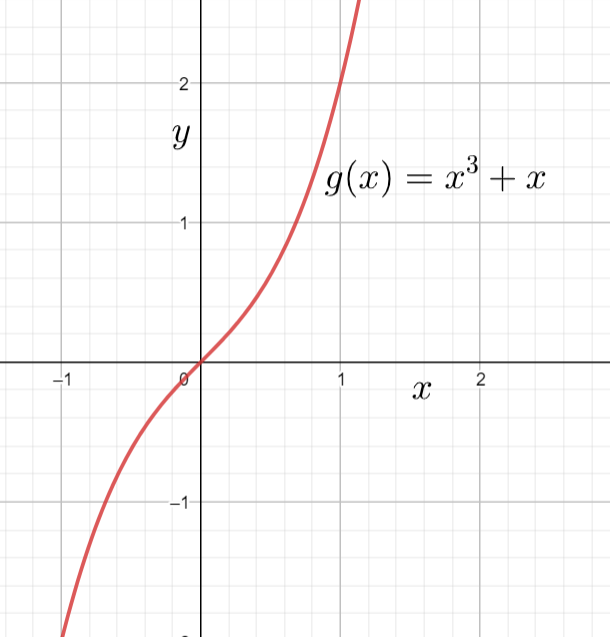
We can also observe that the equation $g\left( x \right)={{x}^{3}}+x$ touches the $x$ axis once. The real roots of the equation $g\left( x \right)={{x}^{3}}+x$ are $x=0$. The multiplicity of the root $0$ is $1$.
From the above two observations we can say that the multiplicity of a real root of an equation which touches the $x$ axis is independent of how many points the equation touches the $x$ axis.
Note: In this problem we have used the term multiplicity of the polynomial. We can define the multiplicity of a polynomial as the occurrence or appearance of a factor in the factorial form of the polynomial. It shows how the graph of the polynomial will look like.
Complete step-by-step solution:
Let us assume the equation $f\left( x \right)={{x}^{3}}$.
The graph of the function $f\left( x \right)={{x}^{3}}$ would be

We can observe that the function $f\left( x \right)={{x}^{3}}$ touches the $x$ axis once. The roots of the equation $f\left( x \right)={{x}^{3}}$ are $x=0,0,0$. The multiplicity of the root $0$ is $3$.
Now let us consider the function $g\left( x \right)={{x}^{3}}+x$. The graph of the equation $g\left( x \right)={{x}^{3}}+x$ is given by
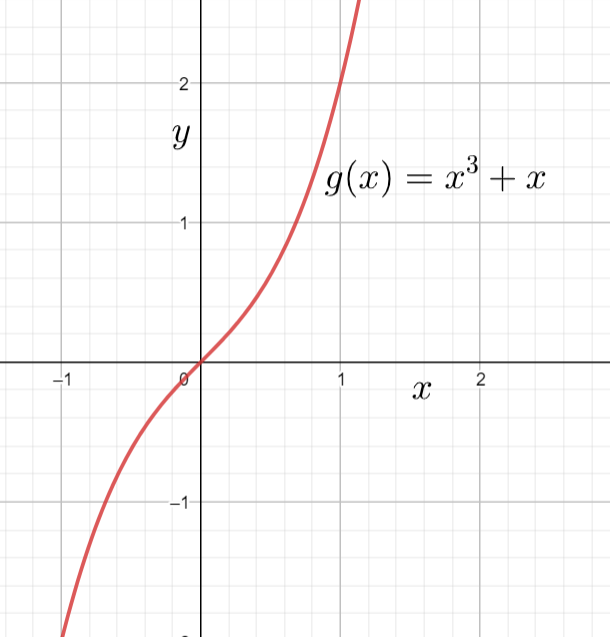
We can also observe that the equation $g\left( x \right)={{x}^{3}}+x$ touches the $x$ axis once. The real roots of the equation $g\left( x \right)={{x}^{3}}+x$ are $x=0$. The multiplicity of the root $0$ is $1$.
From the above two observations we can say that the multiplicity of a real root of an equation which touches the $x$ axis is independent of how many points the equation touches the $x$ axis.
Note: In this problem we have used the term multiplicity of the polynomial. We can define the multiplicity of a polynomial as the occurrence or appearance of a factor in the factorial form of the polynomial. It shows how the graph of the polynomial will look like.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




