Question

Mr Verma (50kg) and Mr Mathur (60kg) are sitting at the two extremities of a 4 m long boat (40kg) standing still in water. To discuss a mechanic problem, they come to the middle of the boat. Neglecting friction with the water, how far does the boat move on the water during the process?

Answer 1

Hint: Centre of mass is the point in a body at which the object can be balanced. At this point, torques of the mass elements will be zero. Use the centre of the mass equation to get the distance travelled by boat due to the shift of the centre of mass.

Complete step by step answer:

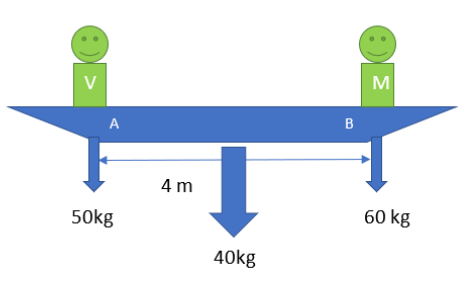
From the question we can conclude that;
Mass of Mr Verma, \[{{m}_{V}}=50kg\]
Mass of Mr Mathur, \[{{m}_{M}}=60kg\]
Mass of the boat, \[{{m}_{B}}=40kg\]
At the initial stage, Mr Verma and Mr Mathur were at the two extreme positions of the boat and we are taking A as the point of origin.
Hence, we can find the distance of the centre of mass at that time.
\[{{X}_{m}}=\dfrac{{{m}_{V}}\times {{x}_{V}}+{{m}_{M}}\times {{x}_{M}}+{{m}_{B}}\times {{x}_{B}}}{{{m}_{V}}+{{m}_{M}}+{{m}_{B}}}\], where \[{{x}_{V}}\], \[{{x}_{M}}\] and \[{{x}_{B}}\] are the distance of Mr Verma, Mr Mathur and boat with respect to the origin.
Initially, they are not moving. So, the distances in metres will be
\[{{x}_{V}}=0\]
\[{{x}_{M}}=4\]
\[{{x}_{B}}=2\]
We can assign these values to the equation
\[{{X}_{m}}=\dfrac{50\times 0+60\times 4+40\times 2}{50+60+40}\]
\[{{X}_{m}}=\dfrac{320}{150}=2.13m\] from point A
Since it is not experiencing any force, the centre of mass will not change. The middle point of the boat is 2m away from point A. When both men move towards the middle of the boat, the centre of mass shifts from 2.13 metre from the origin A.
Therefore, the shift in the centre of mass will be,
\[\Rightarrow 2-2.13=-0.13m\] towards the left.
The negative sign shows that the boat will move 13 cm towards the left of point A. The boat will move 13 cm due to the shift of the centre of mass.

Note: The boat will move 13 cm either to the left or right depending upon the mass distribution in the boat. The centre of mass is very useful since the problems can be simplified by considering the mass of the whole system as a common centre of mass. If we are applying any other external forces to the system, we have to consider that also to find the distance shifted by the boat.