Question

Mr. Verma (50Kg) and Mr. Mathur (60Kg) are sitting at the two extremes of a 4m long boat (40Kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move in the water during the process:
$
  {\text{A}}{\text{. }}\dfrac{{40}}{3}cm \\
  {\text{B}}{\text{. }}\dfrac{{20}}{3}cm \\
  {\text{C}}{\text{. }}\dfrac{{10}}{3}cm \\
  {\text{D}}{\text{. }}10cm \\
$

Answer 1

Hint: Here we go through the property of the center of mass to solve the question by first letting the persons and boat have different systems and then by letting all in the same system.

Complete Step-by-Step solution:
Here in the question it is given that Mr. Verma (50Kg) and Mr. Mathur (60Kg) are sitting at the two extremes of a 4m long boat (40Kg).
Now let,
${M_1} = $ Mass of Mr. Verma=50 kg ${X_1} = $Position of Mr. Verma
${M_2} = $Mass of Boat =40 kg ${X_2} = $Position Of Boat
${M_2} = $Mass of Mr. Mathur= 60 kg ${X_3} = $Position of Mr. Mathur.
Let the coordinate of the position of Mr. Verma be${X_1} \equiv (0,0)$ from this point we can say that the position of boat is ${X_2} \equiv (2,0)$ (because we know in uniform body the centre of mass is in the centre) and ${X_3} \equiv (4,0)$
As we know the formula of Center of mass of system in x is $\dfrac{{{M_1}{X_1} + {M_2}{X_2} + {M_3}{X_3}}}{{{M_1} + {M_2} + {M_3}}}$
After putting the data in the formula we get,
C.O.M. $ = \dfrac{{(50)(0) + (40)(2) + (60)(4)}}{{60 + 40 + 50}} = \dfrac{{32}}{{15}}$

When both come to the middle of the boat the mass of all the body comes to the center of the boat and now we will find out the centre of mass again taking the whole system.

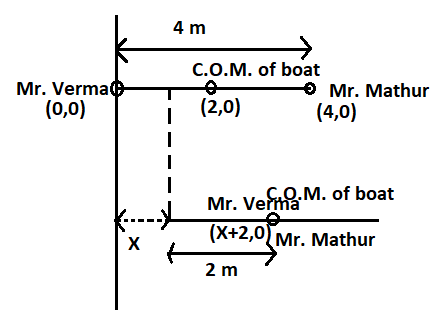
Let the distance moved by the boat be X from the origin.
The final coordinates of the centre of mass of boat, Mr. Verma and Mr. Mathur will be (X+2)
The centre of mass of system will now have equation:
Final C.O.M$ = \dfrac{{(X + 2)(50 + 40 + 60)}}{{50 + 40 + 60}}$
The initial and final C.O.M. will be same:
$\dfrac{{32}}{{15}}$$ = \dfrac{{(X + 2)(50 + 40 + 60)}}{{50 + 40 + 60}}$
From the above equation we get the value of X as
$\dfrac{2}{{15}}meters$
The options are in centimeters so, multiplying by 100 to get the answer:
$\dfrac{2}{{15}} \times 100 = \dfrac{{40}}{3} cm$
This gives (A) as the correct option.

Note- This is a simple centre of mass problem and to solve this type of question, the formula should be correctly remembered plus the diagram should be made to get the correct idea of displacement.