
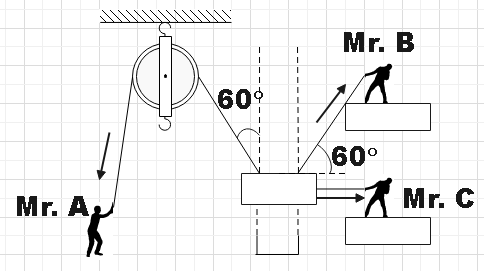
Mr. A, B and C are trying to put a heavy piston into a cylinder at a mechanical workshop in a railway yard. If they apply forces${{F}_{1}}$, ${{F}_{2}}$ and ${{F}_{3}}$ respectively on ropes then for which set of forces at that instant, they will be able to perform the said job?
A. $\sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}$
B. $2{{F}_{1}}={{F}_{2}}+{{F}_{3}}$
C. $2{{F}_{2}}=\sqrt{3}{{F}_{1}}-\dfrac{{{F}_{3}}}{2}$
D. ${{F}_{3}}=2{{F}_{1}}-\sqrt{3}{{F}_{2}}$

Answer
555k+ views
Hint: As a first step, you could go for making a free body diagram for piston marking all the possible forces that are acting on it. You could resolve these forces into their components as per requirement. Then, you could find a condition that will assure the three men completing their task. And thus find the answer.
Complete answer:
In the question we are given three men who are at a mechanical workshop trying to put a heavy piston into a cylinder. The forces applied by Mr. A, Mr. B and Mr. C are given as${{F}_{1}}$, ${{F}_{2}}$ and ${{F}_{3}}$ respectively and their directions are as indicated in the diagram. Now let us make a free body diagram and then resolve all the three forces into their respective components.
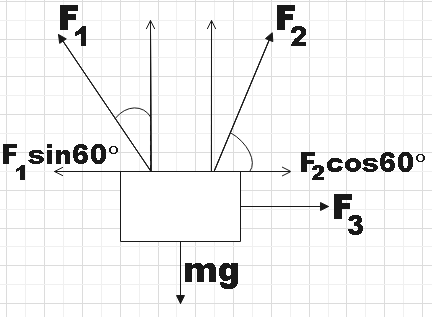
We know that this piston is undergoing only vertical displacement due to all the forces on it and thus we could conclude that the net force in the horizontal direction is zero. Mathematically,
${{F}_{1}}\sin 60{}^\circ -{{F}_{2}}\cos 60{}^\circ -{{F}_{3}}=0$
$\Rightarrow \dfrac{\sqrt{3}{{F}_{1}}}{2}-\dfrac{{{F}_{2}}}{2}-{{F}_{3}}=0$
$\Rightarrow \sqrt{3}{{F}_{1}}-{{F}_{2}}-2{{F}_{3}}=0$
$\therefore \sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}$
So, we have found the condition that ensures that three men will be able to do their job to be,
$\sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}$
Hence, option A is found to be the correct answer.
Note:
You may have noted that the free body diagram is made by giving importance to the horizontal forces acting on the piston. We do have vertical components for the forces and the weight of the body acting downwards. However the net displacement of the piston is obviously downwards and as said in the solution, there is no horizontal displacement.
Complete answer:
In the question we are given three men who are at a mechanical workshop trying to put a heavy piston into a cylinder. The forces applied by Mr. A, Mr. B and Mr. C are given as${{F}_{1}}$, ${{F}_{2}}$ and ${{F}_{3}}$ respectively and their directions are as indicated in the diagram. Now let us make a free body diagram and then resolve all the three forces into their respective components.

We know that this piston is undergoing only vertical displacement due to all the forces on it and thus we could conclude that the net force in the horizontal direction is zero. Mathematically,
${{F}_{1}}\sin 60{}^\circ -{{F}_{2}}\cos 60{}^\circ -{{F}_{3}}=0$
$\Rightarrow \dfrac{\sqrt{3}{{F}_{1}}}{2}-\dfrac{{{F}_{2}}}{2}-{{F}_{3}}=0$
$\Rightarrow \sqrt{3}{{F}_{1}}-{{F}_{2}}-2{{F}_{3}}=0$
$\therefore \sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}$
So, we have found the condition that ensures that three men will be able to do their job to be,
$\sqrt{3}{{F}_{1}}={{F}_{2}}+2{{F}_{3}}$
Hence, option A is found to be the correct answer.
Note:
You may have noted that the free body diagram is made by giving importance to the horizontal forces acting on the piston. We do have vertical components for the forces and the weight of the body acting downwards. However the net displacement of the piston is obviously downwards and as said in the solution, there is no horizontal displacement.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




