Question

How much more water is needed to fill the tank to its brim?

A) $2400{\text{c}}{{\text{m}}^3}$
B) $3200{\text{c}}{{\text{m}}^3}$
C) $3600{\text{c}}{{\text{m}}^3}$
D) $6000{\text{c}}{{\text{m}}^3}$

Answer 1

Hint: Find the volume of the tank in which water is filled by using the formula of the volume of a cuboid, then we have to find the capacity of the tank and then subtract the volume in which the water is filled already.

Complete Step-by-step Solution
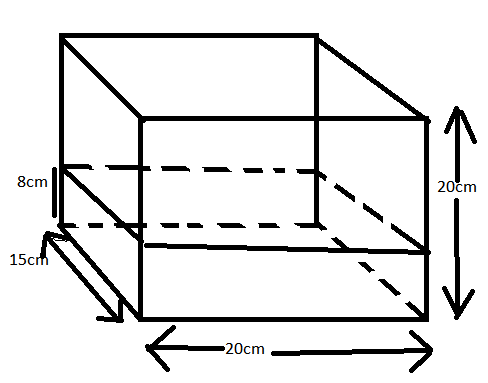
Given: A figure of tank is given in cuboid form in which some of portion of tank is filled. The specification of cuboid is given which is $(20{\text{cm}} \times {\text{8cm}} \times {\text{15cm)}}$ and also the specification of the portion filled with water is given which is $(20{\text{cm}} \times {\text{8cm}} \times {\text{15cm)}}$ .
To find: The volume of the vacuum space of the cuboid is to be found out.
First we will find the volume of cuboid of specification $(20{\text{cm}} \times {\text{8cm}} \times {\text{15cm)}}$
As we know, the volume of cuboid $ = l \times b \times h$
Where length is represented by $l$,breadth is represented by $b$ ,height is represented by $h$ .
Volume of whole cuboid $ = 20 \times 20 \times 15$
$ = 6000{\text{c}}{{\text{m}}^3}$
Now we will find the volume of cuboid which is already filled with specification $(20{\text{cm}} \times {\text{8cm}} \times {\text{15cm)}}$
Volume of cuboid filled already $ = 20 \times 8 \times 15$
$ = 2400{\text{c}}{{\text{m}}^3}$
Now we required the volume of cuboid to be filled to its brim.
So volume of cuboid to be filled $ = $ vol. of whole cuboid $ - $ vol. of cuboid filled already
$ = 6000 - 2400 = 3600{\text{c}}{{\text{m}}^3}$

Hence $3600{\text{c}}{{\text{m}}^3}$ more water is needed to fill the tank to its brim.

Note:
Look at the figure and take a hint from the figure that we required the volume of the vacuum portion and then apply the formula of the volume of a cuboid.