Question

How many more squares must be shaded so that $\dfrac{1}{3}$ of the figure is shaded?

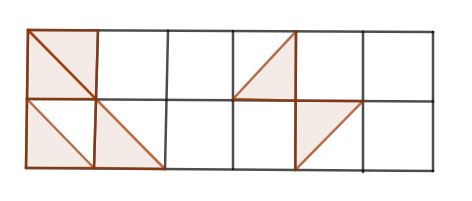
(a) 1
(b) 2
(c) 3
(d) 4

Answer 1

Hint: First of all, we are going to find in the given figure how much portion is shaded from the total. For that count the number of squares present in the given figure. Then count the number of triangles which are shaded in the given figure. From the figure, you can see that two triangles are making one square so from the shaded triangles we can find the number of squares which are shaded. Now, divide the shaded squares to the total squares to find the fraction of portion of the figure which is shaded and then find how many more squares we need to shade so that $\dfrac{1}{3}$ of the figure is shaded.

Complete step by step answer:
The figure given in the above problem is as follows:

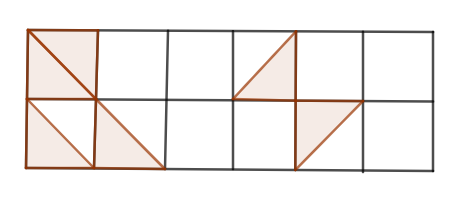
First of all, let us count the number of squares present in the above figure.
The above figure is made up of 2 rows and in each row there are 6 squares so total squares present in two rows are multiplication of 6 by 2 which is equal to:
$\begin{align}
  & 6\times 2 \\
 & =12 \\
\end{align}$
Hence, there are a total 12 squares present in the above figure.
From the above figure, you can see that combining two triangles will make 1 square so we are going to count the number of shaded triangles.
In the upper row of the above figure, there are 3 shaded triangles and in the lower row, there are 3 shaded triangles so total triangles which are shaded is the addition of 3 with 3.
$\begin{align}
  & 3+3 \\
 & =6 \\
\end{align}$
Hence, the total number of triangles which are shaded is 6. Now, calculating the number of squares from these total triangles by dividing total number of triangles by 2 which will give us:
$\begin{align}
  & \dfrac{6}{2} \\
 & =3 \\
\end{align}$
Hence, the total number of shaded squares is 3.
Now, we are going to find the number of shaded squares which we are required so that $\dfrac{1}{3}$ of the figure is shaded.
We have calculated the total squares given in the figure as 12. Now, multiplying 12 by $\dfrac{1}{3}$ we will get the number of squares which are shaded.
$12\times \dfrac{1}{3}$
In the above fraction, 12 is divisible by 3 by 4 times so the simplification of the above expression is:
4
In the above, we have calculated the shaded squares in the given figure as 3 and we require the squares to be shaded as 4 so the required number of squares is calculated by subtracting 3 from 4:
$\begin{align}
  & 4-3 \\
 & =1 \\
\end{align}$
Hence, we must shade 1 square in the given figure so that $\dfrac{1}{3}$ of the figure is shaded.

So, the correct answer is “Option a”.

Note: The possible mistake that could happen is in counting the number of squares so be careful while calculating them. This calculation mistake could be avoided as follows:
As the size of the squares is small so counting them can lead to mistakes so count the total rows and columns in the given figure.
Number of rows in the given figure is 2 and the number of columns are 6 so the number of squares is the number of columns. In this way, counting the number of columns will minimize the possibility of wrong counting.