Question

Moon effect. Some people believe that the Moon controls their activities. If the Moon moves from being directly on the opposite side of Earth from you to being directly overhead, by what percent does the Moon’s gravitational pull on your increase. Assume that the Earth-Moon (center-to-center) distance is \[3.82\times {{10}^{8}}\,m\] and Earth’s radius is \[6.37\times {{10}^{6}}\,m\].

Answer 1

Hint: This question is based on the concept of the gravitational force of attraction/repulsion between the two objects/bodies. By making use of Newton’s law of gravitation, we will be computing the percent increase of the Moon’s gravitation on us, as Newton’s law is a universal law (applicable everywhere).
Formula used:
\[F=G\dfrac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]

Complete step-by-step solution:
From the data, we have,
The Earth-Moon distance, that is, the distance between the moon and the Earth is, \[{{r}_{ME}}=3.82\times {{10}^{8}}\,m\]
The Earth’s radius, that is, the distance from the surface of the Earth and the moon is, \[{{r}_{E}}=6.37\times {{10}^{6}}\,m\]
Newton’s law of gravitation is given by the expression,
\[F=G\dfrac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]
Where \[{{m}_{1}},{{m}_{2}}\]are the masses of the particles, r is the distance between them and G is the gravitational constant, with a value of \[6.67\times {{10}^{-11}}{{{m}^{3}}}/{kg\,{{s}^{2}}}\;\].
The moon and the earth are separated by a great distance such that they can be treated as particles. Thus, we can use Newton’s law of gravitation to solve this problem.
Firstly, we will derive the expressions for the gravitational pull on the body before the change in the gravitational pull is given as follows.
\[{{F}_{1}}=G\dfrac{{{M}_{m}}m}{{{({{r}_{ME}}+{{r}_{E}})}^{2}}}\]
Where \[{{M}_{m}},m\] are the masses of the moon and our body, \[{{r}_{ME}},{{r}_{E}}\] are the earth-moon distance and earth radius distance and G is the gravitational constant.
A diagram representing the given situation is as below.

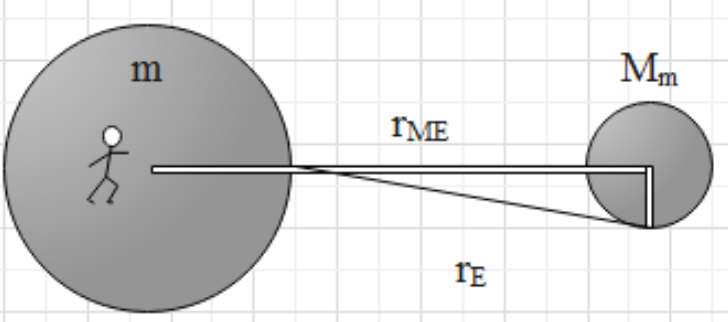
Similarly, we will derive the expressions for the gravitational pull on the body after the change in the gravitational pull is given as follows.
\[{{F}_{2}}=G\dfrac{{{M}_{m}}m}{{{({{r}_{ME}}-{{r}_{E}})}^{2}}}\]
Where \[{{M}_{m}},m\] are the masses of the moon and our body, \[{{r}_{ME}},{{r}_{E}}\] are the earth-moon distance and earth radius distance and G is the gravitational constant.
As the ratio without any kind of change results to 1, thus, subtract one from the ratio of the above forces mentioned.
So, we get,
\[\begin{align}
& \dfrac{{{F}_{2}}}{{{F}_{1}}}-1=\dfrac{G\dfrac{{{M}_{m}}m}{{{({{r}_{ME}}-{{r}_{E}})}^{2}}}}{G\dfrac{{{M}_{m}}m}{{{({{r}_{ME}}+{{r}_{E}})}^{2}}}}-1 \\
 & \Rightarrow \dfrac{{{F}_{2}}}{{{F}_{1}}}-1=\dfrac{{{({{r}_{ME}}+{{r}_{E}})}^{2}}}{{{({{r}_{ME}}-{{r}_{E}})}^{2}}}-1 \\
\end{align}\]
Now, substitute the given values of the distances in the above equation to obtain the percent change in the Moon’s gravitational pull.
\[\begin{align}
  & \dfrac{{{F}_{2}}}{{{F}_{1}}}-1=\dfrac{{{(3.82\times {{10}^{8}}+6.37\times {{10}^{6}})}^{2}}}{{{(3.82\times {{10}^{8}}-6.37\times {{10}^{6}})}^{2}}}-1 \\
 & \Rightarrow \dfrac{{{F}_{2}}}{{{F}_{1}}}-1=0.06898 \\
\end{align}\]
Therefore, the percent increase of the gravitational pull by the change in the Moon’s gravitational pull is $6.898\%.$

Note: The usage of the concept, Newton’s law of gravitation is important, as it is a universal law. The moon and the earth are separated by a great distance such that they can be treated as particles. Thus, we can use Newton’s law of gravitation to solve this problem.