Question

What is the moment of inertia of a solid sphere of mass m and radius R kept with its centre as x-axis at (2R,0) about y-axis?
A. $\dfrac{{44}}{7}m{R^2}$
B. $\dfrac{{22}}{5}m{R^2}$
C. $\dfrac{2}{5}m{R^2}$
D. $\dfrac{2}{3}m{R^2}$

Answer 1

Hint: Whenever a body is set into motion, it is observed that the body will not respond quickly to the rotation. This is due to the fact there is something called inertia which indicates the inability to adapt to the quick change in the state of the body. When this inertia is associated with rotation, we call it a moment of inertia.
Usually, the standard moment of inertia of a body is defined by a fixed formula for every geometric shape at a particular standard axis. To calculate the moment of inertia through another axis other than the standard one, we have to use two theorems, namely, Parallel axis theorem and Perpendicular axis theorem.

Complete step-by-step answer:
The moment of inertia basically, gives us the distribution of mass of a body around its axis of rotation and it is the quantity that determines the torque required to produce an angular acceleration in the rotating body.
Consider a sphere of mass m and radius R resting on the line XX with its axis being YY.

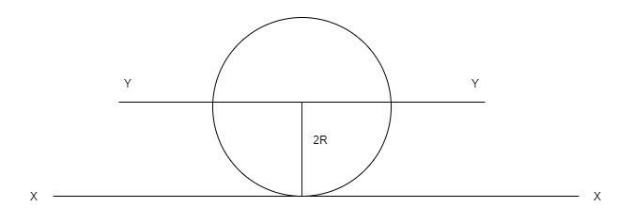
The moment of inertia of a sphere about its centre-axis.
${I_{YY}} = \dfrac{2}{5}m{R^2}$
The moment of inertia about the point (0,2R) on the y-axis or line XX is calculated by using the Parallel axis theorem which states that - The moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of body about the axis passing through the centre and product of mass of the body times the square of distance between the two axes.
${I_{XX}} = {I_{YY}} + m{d^2}$
Substituting, we get –
$
  {I_{XX}} = \dfrac{2}{5}m{R^2} + m{\left( {2R} \right)^2} \\
  Solving, \\
  {I_{XX}} = \dfrac{2}{5}m{R^2} + 4m{R^2} \\
   \to {I_{XX}} = m{R^2}\left( {\dfrac{2}{5} + 4} \right) \\
  Solving, \\
  {I_{XX}} = m{R^2}\left( {\dfrac{{2 + 20}}{5}} \right) \\
  \therefore {I_{XX}} = \dfrac{{22}}{5}m{R^2} \\
 $

Hence, the correct option is Option B.

Note: There are 2 ways of compressive stress failure in columns – Crushing and Buckling. Crushing occurs for shorter columns, also called struts and Buckling occurs in longer columns. Even though you may think that their classification of long and short columns is subjective, it depends on a number known as Slenderness Ratio, which is dependent on moment of inertia.
Slenderness ratio = $\dfrac{l}{k}$
where $l$= effective length of the column
and $k$= radius of gyration.
The radius of gyration, $k = \sqrt {\dfrac{I}{A}} $
where $I$ is the least moment of inertia of the cross-section of the column and A is the area of cross-section.