Question

What is the molecular geometry of $SbC{l}_3$ ?

Answer 1

Hint: We have to know that the molecular geometry is the three-dimensional plane of the iotas that establish a particle. It incorporates the overall state of the particle just as security lengths, security points, torsional points, and whatever other mathematical boundaries that decide the situation of every atom.

Complete answer:
We have to know, some steps used to find the shape of the molecule that has to be given,
To summarize there are four straightforward strides to apply the VSEPR hypothesis.
First, we have to draw the Lewis structure.
Then, check the quantity of electron gatherings and recognize them as bond sets of electron gatherings or solitary sets of electrons. Recollect electron bunches incorporate securities as well as solitary sets!
Now, name the electron-bunch calculation. (State whether it is straight, three-sided planar, tetrahedral, three-sided bipyramidal, or octahedral.)
Finally, taking a gander at the places of other nuclear cores around the focal points decides the sub-atomic math. (Perceive the number of solitary sets there are.)
Molecular geometry impacts a few properties of a substance including its reactivity, extremity, period of issue, shading, attraction, and organic movement. The points between bonds that a particle structures depend just feebly on the remainder of the atom, for example they can be perceived as around nearby and henceforth adaptable properties.
The Lewis structure of $SbC{l}_3$ has to be drawn below,

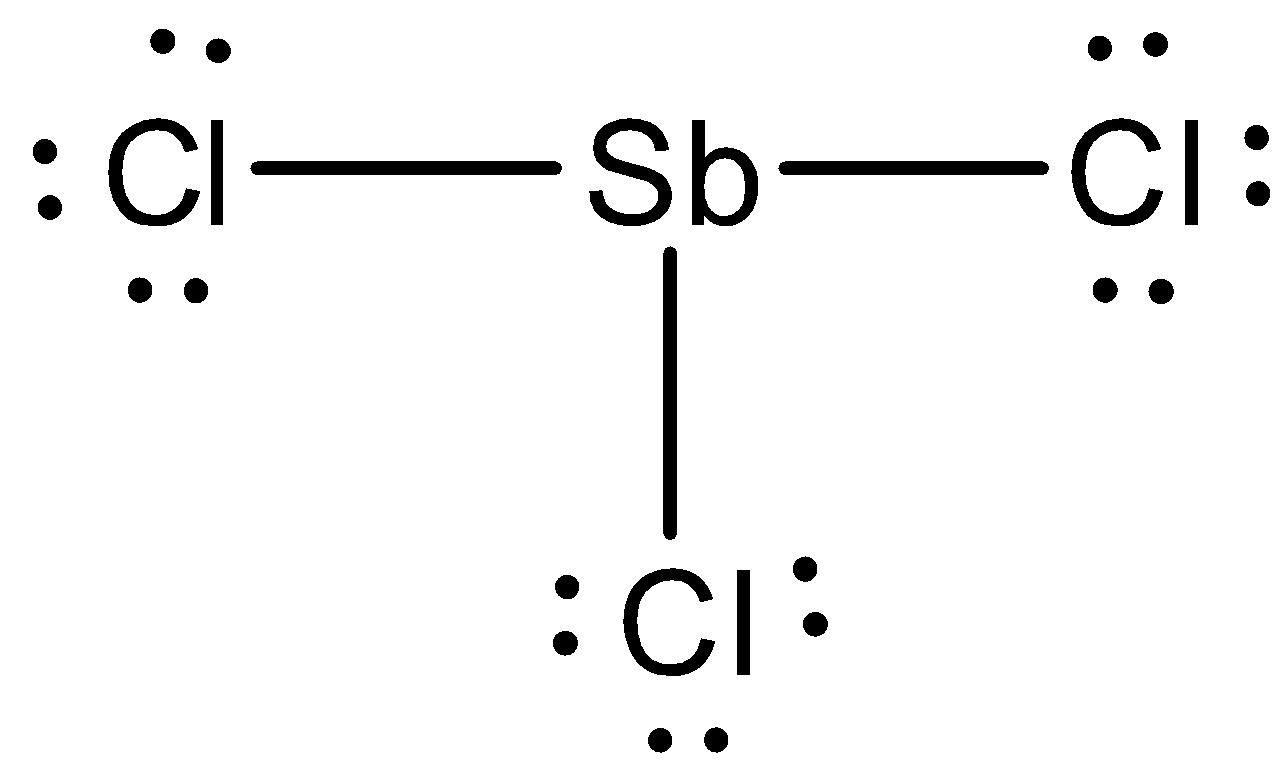
We have to find out the molecular geometry of $SbC{l}_3$ , around the focal tin particle, there are four electron sets, three are holding, and one non-holding. Therefore, the molecular geometry is trigonal pyramidal.

Note:
We have to know that, the reason for the VSEPR hypothesis is that electron sets situated in bonds and solitary sets repulse one another and will along these lines receive the math that places electron sets as far separated from one another as could really be expected.