Question

Minimum numbers of unequal vectors which can give zero resultant are:
A. Two
B. Three
C. Four
D. More than four

Answer 1

Hint: Consider the case of two vectors and check whether their resultant will be zero or not. If not then consider three vectors, and examine how they can have zero resultant. Do not put the vectors parallel or perpendicular to each other.

Complete step by step solution:
We know that unequal vectors mean vectors with different magnitudes.
If we have two vectors, the resultant of these two vectors is zero when the direction of these two vectors is opposite to each other. Also, the resultant will be zero, if and only if they have the same magnitude. So, we can say two non-zero vectors with the same magnitude give zero resultant. But we have given that the vectors should be unequal. Therefore, the option (A) is incorrect.
Now, we have three vectors A, B and C such that none of them is parallel to each other as shown in the figure below.

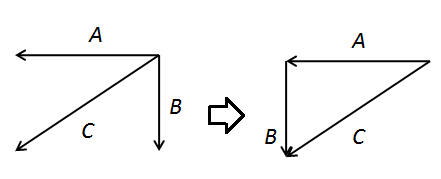
Here, C is the resultant of vectors A and B.
From the above figure, we can write,
$$C=-A-B$$
Now, the resultant of the three vectors A, B and C is,
$$A+B+C=A+B+\left(-A-B\right)$$
$$\Rightarrow A+B+C=0$$
Therefore, if we have three vectors, the resultant can be zero.

So, the correct answer is “Option B”.

Note:
Students should note that zero vector is also a vector whose result is zero. But since it has zero magnitude, we did not take it into account. Four equal vectors each of them perpendicular to each other will give zero resultant if and only if they have equal magnitudes. Therefore, you should note that, for the resultant to be zero, the unequal vectors should not be parallel or perpendicular to each other.