Question

What minimum is to be pulled Contacts \[15\]. I’ll be force by the rod on one of the blocks \[20\]. A block of mass M is kept on a rough horizontal surface. The coefficient of static friction between the block and the surface is\[\mu \]. The block is to be pulled by applying a force to it. What minimum force is needed to side the block? In which direction should this block force act? The friction coefficient, between the board and the floor block? In what motion should I be bored?

Answer 1

Hint: The coefficient of friction is a dimensionless scalar value. The coefficient of friction is a ratio of the force friction between two bodies and force pressing together. Friction does not depend on the amount of surface area in contact between moving bodies. Friction depends on the magnitude of the forces holding the bodies together. The coefficients of friction range from \[0\] to greater than 1.

Complete step-by-step solution:

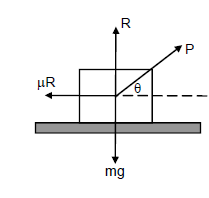
Let ‘\[P\] ’ be the force applied to at an angle \[\theta \] from the free body diagram.
\[R + P\sin \theta - mg = 0\]
\[R = - P\sin \theta + mg \to \left( 1 \right)\]
\[\mu R - P\cos \theta \to \left( 2 \right)\]
Equation \[\left( 1 \right)\mu \left( {mg - P\sin \theta } \right) - P\cos \theta = 0\]
\[ \Rightarrow \mu mg = \mu \rho \sin \theta - P\cos \theta \Rightarrow \rho = \dfrac{{\mu mg}}{{\mu \sin \theta + \cos \theta }}\]
Applied force \[P\] should be minimum, when \[\mu \sin \theta + \cos \theta \] is maximum again, \[\mu \sin \theta + \cos \theta \] is maximum when its derivative is zero.
Therefore, \[d/d\theta \left( {\mu \sin \theta + \cos \theta } \right) = 0\]
\[\mu \cos \theta - \sin \theta = 0\]
\[\theta = {\tan ^{ - 1}}\mu \]
So,\[P = \dfrac{{\mu mg}}{{\mu \sin \theta + \cos \theta }} = \dfrac{{\mu mg/\cos \theta }}{{\dfrac{{\mu \sin \theta }}{{\cos \theta }} + \dfrac{{\cos \theta }}{{\cos \theta }}}} = \dfrac{{\mu mg\sec \theta }}{{1 + \mu \tan \theta }} = \dfrac{{\mu mg\sec \theta }}{{1 + {{\tan }^2}\theta }}\]
\[ = \dfrac{{\mu mg}}{{\sec \theta }} = \dfrac{{\mu mg}}{{\sqrt {\left( {1 + {{\tan }^2}\theta } \right)} }} = \dfrac{{\mu mg}}{{\sqrt {1 + {\mu ^2}} }}\]
The minimum force is \[\dfrac{{\mu mg}}{{\sqrt {1 + {\mu ^2}} }}\] at an angle \[\theta = {\tan ^{ - 1}}\mu \].
The block should move in the direction of the larger force. So, the block moves to the left side.
The friction coefficient between the board and floor is \[\mu \]. Therefore the maximum friction force which the floor can exert is \[\mu N\], when \[N\] is the normal reaction at the contact surface between the board and the floor.

Note:The static coefficient of friction is applied to motionless objects. The low value of the coefficient of friction is that the force required for sliding occurs is less than the force required when the coefficient of friction is high. The coefficients of friction range from \[0\] to greater than 1.