Question

Midpoint of the line segment joining the points \[\left( { - 5,4} \right)\] and \[\left( {9, - 8} \right)\] is
A.\[\left( { - 7,6} \right)\]
B.\[\left( {2, - 2} \right)\]
C.\[\left( {7, - 6} \right)\]
D.\[\left( { - 2, - 2} \right)\]

Answer 1

Hint: Here, we will use the midpoint formula to find the midpoint of the segment. We will find the sum of the \[x\]- coordinates and \[y\]- coordinates of the two points separately. Then we will divide the obtained sums by 2. This will give us the \[x\]- coordinate (abscissa) and \[y\]- coordinate (ordinate) of the midpoint respectively.

Complete step-by-step answer:
If we have to find the midpoint of a line segment whose end coordinates are given, we can use the midpoint formula. If the end-points of the line segment are \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\]. Then the \[x\]- coordinate of the midpoint will be \[\dfrac{{{x_1} + {x_2}}}{2}\] and \[y\]- coordinate of the midpoint will be \[\dfrac{{{y_1} + {y_2}}}{2}\].
Now we will substitute \[ - 5\] for \[{x_1}\], 9 for \[{x_2}\], 4 for \[{y_1}\] and \[ - 8\] for \[{y_2}\] in the midpoint formula \[\dfrac{{{x_1} + {x_2}}}{2}\] and \[\dfrac{{{y_1} + {y_2}}}{2}\].
\[x = \dfrac{{ - 5 + 9}}{2} = 2\]
\[y = \dfrac{{4 - 8}}{2} = - 2\]
$\therefore $ The midpoint of the line segment is \[\left( {2, - 2} \right)\]. Hence, option B is the correct option.

Note: We can also find the midpoint using the section formula. The midpoint formula is a special case of the section formula when a point divides a line segment in 2 equal halves (ratio of 1:1).

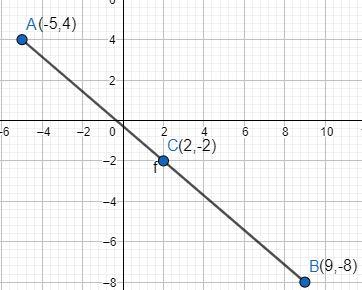
According to the section formula, if a point \[\left( {x,y} \right)\] divides a line segment joining the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\]in the ratio \[m:n\], then \[x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}}\] and \[y = \dfrac{{m{x_2} + n{x_1}}}{{m + n}}\].
We will substitute 1 for \[m\], 1 for \[n\], \[ - 5\] for \[{x_1}\], 9 for \[{x_2}\], 4 for \[{y_1}\] and \[ - 8\] for \[{y_2}\]in the formula \[x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}}\] and \[y = \dfrac{{m{x_2} + n{x_1}}}{{m + n}}\].
\[x = \dfrac{{1 \times 9 + 1 \times \left( { - 5} \right)}}{{1 + 1}} = \dfrac{4}{2} = 2\]
and
\[y = \dfrac{{1 \times 4 + 1 \times \left( { - 8} \right)}}{{1 + 1}} = \dfrac{{ - 4}}{2} = - 2\]
So the coordinates points will be \[\left( {x,y} \right) \equiv \left( {2, - 2} \right)\].