Question

How many metres of cloth of 1.1 m width will be required to make a conical tent whose vertical height is 12 m and base radius is 16 m? Find also the cost of the cloth used at the rate of Rs. 23 per metre.

Answer 1

Hint: Here the total cloth required will be equal to the curved surface area of the conical tent formed. We may assume the length of cloth to be ‘L’ and equate the area of the cloth with the curved surface area of the tent to get the value of ‘L’. After that to find the total cost of the cloth used we may multiply the area of cloth used by the rate per meter.

Complete step-by-step answer:

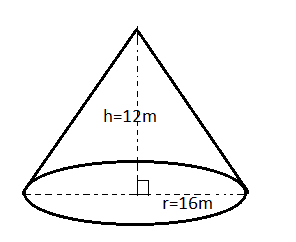
Let us find the curved surface area of the cone. So, the formula that we will use to find the curved surface area of tent is:
$CSA=\pi \times radius\times slant\,height\,of\,cone$
Now, the slant height of cone in terms of radius and height is given as:
$Slant\,height=\sqrt{{{r}^{2}}+{{h}^{2}}}$
Since, it is given that the radius of the cone is 16 m and the height of the cone is 12 m. So, slant height will be:
$\begin{align}
  & Slant\,height=\sqrt{{{16}^{2}}+{{12}^{2}}} \\
 & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\sqrt{256+144}\, \\
 & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\sqrt{400} \\
 & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=20\,m \\
\end{align}$
Therefore, curved surface area of this cone is:
$\begin{align}
  & CSA=\pi \times 16\times 20 \\
 & \,\,\,\,\,\,\,\,\,\,=3200\pi \,{{m}^{2}} \\
\end{align}$
Let us consider the length of required cloth = L
Since, the width of the cloth is 1.1 m. So, the area of the cloth required will be = $L\times 1.1\,{{m}^{2}}$
Now, we may equate the curved surface area of the cone and the area of cloth required to get the value of l. So:
$\begin{align}
  & L\times 1.1\,{{m}^{2}}=3200\pi \,{{m}^{2}} \\
 & L=\dfrac{3200\times 3.14}{1.1}=\dfrac{10,048}{1.1}=9,134.54\,m \\
\end{align}$
Hence, the length of the cloth required is = 9134.54 m.
Since, the cost of 1 m of cloth is = Rs. 23
So, the total cost of 9134 m of cloth is =$Rs.9134.54\times 23=Rs.2,10,094.42$.
Hence, the total cost of cloth is Rs. 2,10,094.42.

Note: Students should keep in mind that we have to equate the curved surface area of the cone with the total area of the cloth required and the formula for CSA of cone should be applied carefully. Using vertical height in the formula instead of slant height will lead to a mistake.