Question

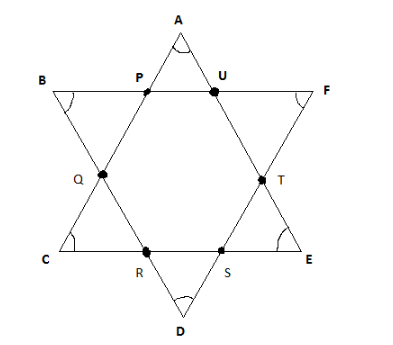
What is the measure of\[\angle A + \angle B + \angle C + + \angle D + \angle E + \angle F\]in the figure given below? Give reason to your answer.

Answer 1

Hint: Sum of the interior angles of a triangle is equal to\[{180^ \circ }\]. An angle is defined as the figure formed by two rays when they meet at a common point. Angle is measured in degrees by using a protractor.
In this question we are asked to find the sum of interior angles of the given figure but from the given figure it is not possible to find the sum of angles so will try to break this figure into a geometrical figure then we will find the sum of angels.

Complete step-by-step answer:
We can see the given figure is a combination of two equilateral triangles where one triangle is ACE and the other is BDF.
We know sum of the interior angles of a triangle is equal to\[{180^ \circ }\]
So in \[\Delta ACE\]by angle sum property we can write
\[\angle A + \angle C + \angle E = {180^ \circ } - - (i)\]
Now similarly in \[\Delta BDF\] by angle sum property we can write
\[\angle B + \angle D + \angle F = {180^ \circ } - - (ii)\]
Now add equation (i) and (ii) together, we get
 \[
\Rightarrow \angle A + \angle C + \angle E + \angle B + \angle D + \angle F = {180^ \circ } + {180^ \circ } \\
  \angle A + \angle B + \angle C + \angle D + \angle E + \angle F = {360^ \circ } \;
 \]
Hence the measure of measure of\[\angle A + \angle B + \angle C + + \angle D + \angle E + \angle F\]is equal to \[ = {360^ \circ }\]

Note: Students must note that whenever we are given any complex figure to find their missing data or to find their area, perimeters we must always try to break that given figure in a regular geometrical shape as it makes it easy to find required values.