Question

What is the measure of the radius of the circle inscribed in a triangle whose sides measure 8 cm, 15 cm and 17cm?
A. 6
B. 2
C. 5
D. 3
E. 7

Answer 1

Hint: The formula of finding the radius of a circle which is inscribed in a triangle with a, b and c side lengths is
r \[=\sqrt{\dfrac{(s-a)(s-b)(s-c)}{s}}\]
(Where ‘r’ is the radius of a circle which is inscribed in a triangle with a, b and c side lengths and s is the semi-perimeter that is s \[=\dfrac{a+b+c}{2}\] )

Complete Step-by-step answer:
As mentioned in the question, we can take ‘a’ as 8, ’b’ as 15 and ‘c’ as 17.

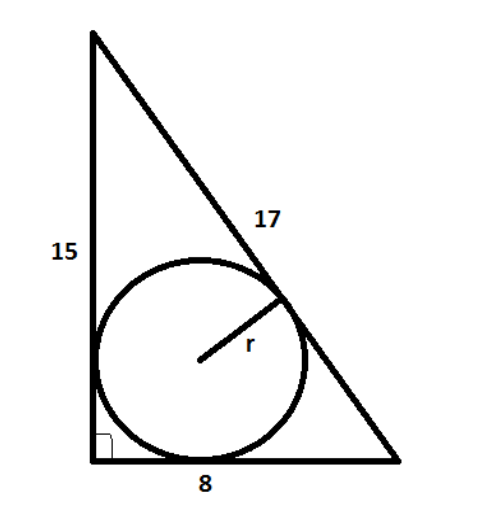
Now, in the formula mentioned in the hint, we need to just put the values in it and we will get the radius of the circle which is inscribed in a triangle with 8, 15 and 17 side lengths and with semi-perimeter as 20 cm is
\[\begin{align}
  & =\sqrt{\dfrac{(20-8)(20-15)(20-17)}{20}} \\
 & =\sqrt{\dfrac{12\times 5\times 3}{20}} \\
 & =3 \\
\end{align}\]
 Hence, the radius of that circle is 3 cm.

Note: Another method to go about this question is that
\[A=\dfrac{sr}{2}\] (Where A is the area of the triangle and s is the semi perimeter and r is the radius of the triangle)
Now, here the area of the triangle can be calculated by Heron’s formula that is
\[A=\sqrt{s(s-a)(s-b)(s-c)}\] (Where s is the semi perimeter and a, b and c are the three sides of the triangle)