Question

What is the measure of angle in degrees between north and West?

Answer 1

Hint: We are provided two directions north and west and we have to find the angle between two directions.
To do this we will use some basic concepts of angles. We know that angles are the combination of two rays coming from a common point.
Firstly, we need to draw all the four directions in $$2D$$ to make it clearer, we know that the straight line always makes $${180}^0$$ angle and the perpendicular line always make $${90}^0$$ angle. So, drawing the $$2D$$ representation of direction will make it clear.

Complete step-by-step answer:
Here we have two directions: north and west
So, firstly we will draw $$2D$$ representation of all four directions.

Here we can see that the north and south directions are forming a straight line so as discussed, they will always form $${180}^0$$ at an angle. but we have to find an angle between the north and west directions. We can see that the north and west directions are perpendicular to one another. So, the angle between the north and west direction is $${90}^0$$.

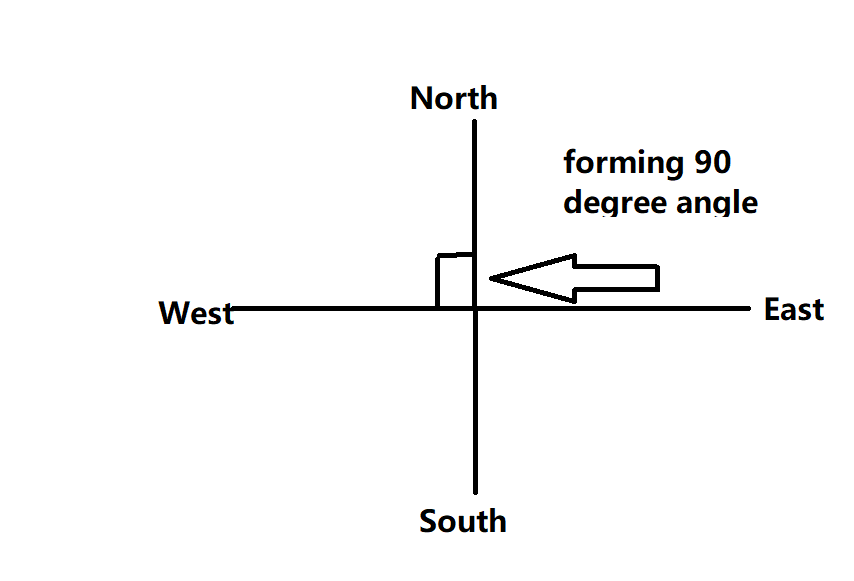
We can see the above observation through the figure drawn above.
FINAL ANSWER: Therefore, we can conclude that the angle between north and west direction is $${90}^0$$.

Note: Students must be careful while drawing figures as they are always confused about directions especially in the case of west and east directions. West is always on the left side and east is always on the right side.
Student must note that straight line that is $${180}^0$$ angle always has its arms in the opposite direction and also two perpendicular line forms four right angles so, in this case, also we have four right angles
It is an angle made by two rays that are perpendicular to each other. The measure of this angle is always $${90}^0$$