Question

What is meant by banking on the road? What is the need of banking on roads? Obtained an expression for the maximum speed with which a vehicle can safely negotiate a curved road banked at an angle $\theta $. The coefficient of friction between the wheels and the road is $\mu $.

Answer 1

Hint: When roads are slanting, they are said to be banked. Banking of roads is needed to increase safety while taking a turn. To obtain an expression for the maximum speed first draw all the forces acting on a vehicle taking a turn on the banked road. Resolve all the forces in the horizontal and vertical components. Equate the net force in the vertical direction to zero. Then equate the horizontal force to $F=ma=\dfrac{m{{v}^{2}}}{r}$. Perform some operations and find the expression for v.

Formula used:
$f=\mu N$
F = ma
$a=\dfrac{{{v}^{2}}}{r}$

Complete answer:
Banking of the road is raising the outer end of the road higher than the inner end. In simple words, banking on the road is making its surface slant.
When a vehicle takes a turn on a flat curved road, it must undergo a circular motion. Therefore, the vehicle must have a centripetal acceleration. This acceleration is provided by the frictional force between the vehicle and the road. However, the frictional force is limited. When the road is banked, the normal reaction by the ground also contributes to the centripetal force. Thus, the value of maximum speed for a safe turn increases.
Let us find an expression for the maximum speed for a safe turn on a curved road banked at an angle $\theta $.
Consider a vehicle taking a turn at a speed v on the banked road. Let the curve be an arc of a circle of radius r. Let us first draw all the forces acting on the vehicle as shown below.

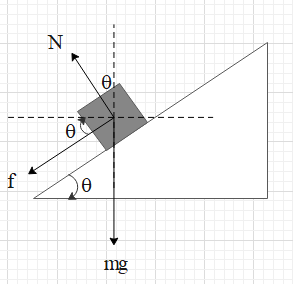
Resolve the normal force and frictional force into their horizontal and vertical components as shown.

The vehicle does not accelerate vertically. Therefore, the net force in the vertical direction is zero.
i.e. $N\cos \theta =mg+f\sin \theta $ …. (i)
The value of frictional force is given as $f=\mu N$.
Substitute the value of f in equation (i).
$\Rightarrow N\cos \theta =mg+\mu N\sin \theta $
$\Rightarrow N=\dfrac{mg}{\cos \theta -\mu \sin \theta }$
And $f=\mu N=\dfrac{\mu mg}{\cos \theta -\mu \sin \theta }$
The net force in the horizontal direction is $F=N\sin \theta +f\cos \theta $ … (ii).
And this force F is the centripetal force acting on the vehicle.
From Newton’s second law, F = ma. Here is the centripetal acceleration.
Centripetal acceleration of a body is given as $a=\dfrac{{{v}^{2}}}{r}$.
Therefore, $F=ma=\dfrac{m{{v}^{2}}}{r}$ …. (iii).
On equating (ii) and (iii), we get
$\dfrac{m{{v}^{2}}}{r}=N\sin \theta +f\cos \theta $
Substitute the values of f and N.
$\Rightarrow \dfrac{m{{v}^{2}}}{r}=\left( \dfrac{mg}{\cos \theta -\mu \sin \theta } \right)\sin \theta +\left( \dfrac{\mu mg}{\cos \theta -\mu \sin \theta } \right)\cos \theta $
$\Rightarrow \dfrac{m{{v}^{2}}}{r}=\left( \dfrac{mg\sin \theta +\mu mg\cos \theta }{\cos \theta -\mu \sin \theta } \right)$
$\Rightarrow {{v}^{2}}=rg\left( \dfrac{\sin \theta +\mu \cos \theta }{\cos \theta -\mu \sin \theta } \right)$
$\Rightarrow {{v}^{2}}=rg\left( \dfrac{\tan \theta +\mu }{1-\mu \tan \theta } \right)$
$\Rightarrow v=\sqrt{rg\left( \dfrac{\tan \theta +\mu }{1-\mu \tan \theta } \right)}$
Hence, we found the expression for the maximum speed for a safe turn.

Note:
The maximum possible speed while taking a turn depends on the way the road is banked. That is the maximum safe speed depends on the angle $\theta $.
Consider the final expression of v, i.e. $v=\sqrt{rg\left( \dfrac{\tan \theta +\mu }{1-\mu \tan \theta } \right)}$.
The maximum value of $\left( \dfrac{\tan \theta +\mu }{1-\mu \tan \theta } \right)$ will give us the maximum possible speed. And that will happen when $\tan \theta =\dfrac{1}{\mu }$.