Question

What is meant by a system of inequalities?

Answer 1

Hint: We can understand the system of inequalities by understanding some basic terminology. With the help of an example, we can solve a system of inequalities and draw individual graphs. We can then select the required area.

Complete step-by-step solution:
We know that a system of inequalities is a set of two or more inequalities which may contain one or more than one variable. We can also say that a system of inequalities is an analogous form of a system of equations, where instead of having equations, we have inequalities which are needed to be solved simultaneously.
Also, we are very clear that the systems of inequalities are used when a problem requires a range of solutions, and there is more than one constraint on these solutions.
A system of inequalities may sometimes contain a union of two or more inequalities. We know that a union means that we have to select those solutions that occur in either one of them.
A system of inequalities may sometimes contain an intersection of two or more inequalities. We know that an intersection means that we have to select only those solutions that occur in both of them.
We can solve a system of inequality by graphing each inequality individually, and then finding the overlaps of these solutions. Let us assume the following system of inequality.
$\begin{align}
  & 2x-3y\le 12 \\
 & x+5y\le 20 \\
 & x>0 \\
\end{align}$
Let us first solve these inequalities. Thus, we get
$\begin{align}
  & y\ge \dfrac{2}{3}x-4 \\
 & y\le -\dfrac{1}{5}x+4 \\
 & x>0 \\
\end{align}$
Let us now graph these inequalities and mark the corresponding areas.
For $y\ge \dfrac{2}{3}x-4$, we have

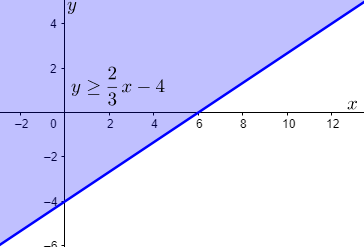
For $y\le -\dfrac{1}{3}x+4$, we have

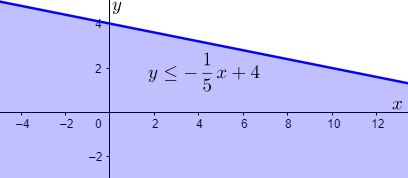
For $x>0$, we have

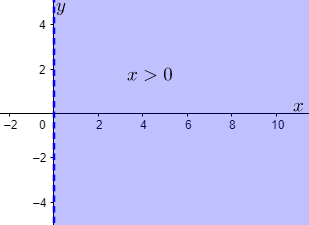
Since, our solution must satisfy all three inequations, we must take the intersection of all these 3 areas.

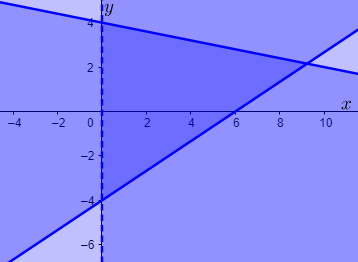
Hence, we can see that the area of intersection is

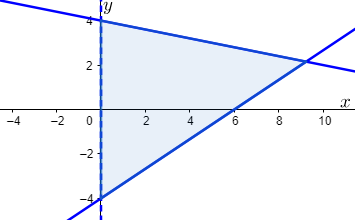
All the points within this enclosed area will be a solution for this system of inequalities.

Note: We must note here that the dotted line in $x>0$, represents that $x=0$ is not included in this solution. Also, we must take care while drawing the individual graphs and selecting the required area. A simpler way to understand this is by selecting a point and seeing whether that lies in the area or not.