Question

What is the meaning of the following symbol in triangle?
$$\cong$$
(A). Degree
(B). Angle
(C). Congruent
(D). Similar

Answer 1

Hint: In this question it is given that we have to find the meaning of the symbol $$\cong$$ which is used in the chapter triangle. So to know about this symbol you should go to your triangle chapter where you can see this symbol ($$\cong$$) is very oftenly used.

Complete step-by-step solution:
Let us consider $$\triangle ABC$$ and $$\triangle DEF$$ be two triangle.

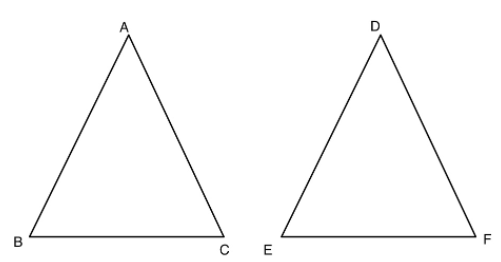
If their corresponding sides and angles are equal to each other then we can say that the triangle are congruent to each other,
i.e, $$\triangle ABC$$ congruent to $$\triangle DEF$$
If we write the above symbolically, then we can write,
$$\triangle ABC\cong \triangle DEF$$
So we can say that $$\cong$$ the symbol of congruent.
Hence the correct option is option C.

Note: In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
More formally, two sets of points are called congruent if, and only if, one can be transformed into the other by an isometry, i.e., a combination of rigid motions, namely a translation, a rotation, and a reflection. This means that either object can be repositioned and reflected (but not resized) so as to coincide precisely with the other object. So two distinct plane figures on a piece of paper are congruent if we can cut them out and then match them up completely. Turning the paper over is permitted.
Also if two line segments are congruent if they have the same length, two angles are congruent if they have the same measure and two circles are congruent if they have the same diameter. So basically congruent is equivalent to equal.