Question

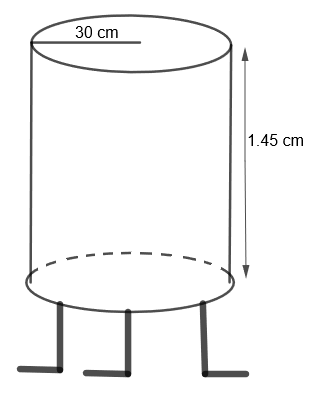
Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45m and its radius is 30 cm. Find the total surface area of the bird-bath.

Answer 1

Hint: First of all, draw the given bird-bath. So the total surface area of bird-bath = curved surface area of the cylinder + curved surface area of the hemisphere. Use the curved surface area of the cylinder \[=2\pi rh\] and the curved surface area of the hemisphere \[=2\pi {{r}^{2}}\] to find the total area of the bird-bath.

Complete step-by-step answer:
We are given a bird-bath in the shape of a cylinder with hemispherical depression at one end. Also, the height of the cylinder is 1.45 m and the radius is 30 cm. We have to find the total surface area of the bird-bath. Let us first see the bird-bath diagrammatically

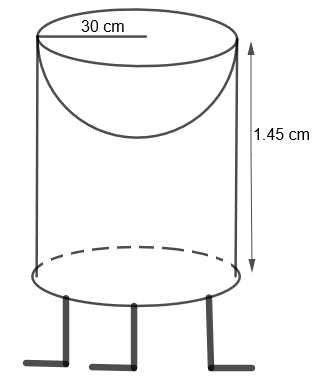
Here, we have to find the total surface area of the bird-bath. So, we get the total surface area of the bird-bath = curved surface area of the cylinder + curved surface area of the hemisphere.
Let us consider the curved surface area of the cylinder as ‘C’ and the curved surface of the hemisphere as ‘H’. So, we get, the total surface area of the bird-bath, S = C + H …..(i)
Now, let us first find the curved surface area of the cylinder. We know that the curved surface area of the cylinder \[=2\pi rh\] where r is the radius and h is the height of the cylinder.
Also, we are given that the radius = 30 cm and height \[=1.45\times 100=145cm\]
So, by substituting the value of radius (r) and height (h), we get,
\[C=2\pi .\left( 30 \right).145c{{m}^{2}}\]
\[C=8700\pi \text{ }c{{m}^{2}}\]
Now, let us find the curved surface area of the hemisphere. We know that the curved surface area of the hemisphere, \[H=2\pi {{r}^{2}}\].
By substituting the value of r = 30 cm, we get,
\[\begin{align}
  & H=2\pi .{{\left( 30 \right)}^{2}}c{{m}^{2}} \\
 & H=1800\pi \text{ }c{{m}^{2}} \\
\end{align}\]
Now, by substituting the value of \[C=8700\pi \text{ }c{{m}^{2}}\] and \[H=1800\pi \text{ }c{{m}^{2}}\] in equation (i), we get,
The total surface area of the bird-bath,
\[\begin{align}
  & S=\left( 8700\pi +1800\pi \right)c{{m}^{2}} \\
 & S=10500\pi \text{ }c{{m}^{2}} \\
\end{align}\]
By substituting the value of \[\pi =\dfrac{22}{7}\], we get,
\[\begin{align}
  & S=10500.\left( \dfrac{22}{7} \right)c{{m}^{2}} \\
 & S=33000\text{ }c{{m}^{2}} \\
 & \Rightarrow S=33000.\dfrac{1}{100}.\dfrac{1}{100}{{m}^{2}} \\
 & S=3.3{{m}^{2}} \\
\end{align}\]
Hence, we get the total surface area of the bird-bath \[=33000c{{m}^{2}}=3.3{{m}^{2}}\]

Note: In this question, students often make this mistake of taking the values of radius and height in different units as it is given. But this is wrong. Students must convert all the parameters in 1 unit like we have taken both the radius and height in cms and then only solve the question to get the desired answer. Also, in these types of questions, always draw a proper diagram because then the question will be easier to visualize and to proceed with.