Question

What is the maximum volume of an open box with a square base whose surface area (not including the top) is 27 $\text{i}{{\text{n}}^{2}}$?

Answer 1

Hint: Let us assume an open box, with a square base with each edge of length a inch, and height of the box h inch.

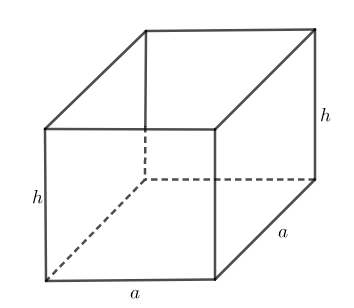
Let the surface area of the box (not including the top the top) be s, then we have
$s=\left( a\times a \right)+4\left( a\times h \right)$
Thus, the surface area of the open box is $s={{a}^{2}}+4ah$.
We can also write the above equation as
 $4ah=s-{{a}^{2}}$
And thus, we have the height of the open box as
$h=\dfrac{s-{{a}^{2}}}{4a}...\left( i \right)$

Complete step-by-step solution:
From the figure, we can clearly say that the volume of this open box is
$V=a\times a\times h$
Using the value of height from equation (i), we get
$V={{a}^{2}}\left( \dfrac{s-{{a}^{2}}}{4a} \right)$
We can simplify this equation by cancelling terms to get,
$V=\left( \dfrac{as-{{a}^{3}}}{4} \right)...\left( ii \right)$
Here, we know that the value of s is constant, and we need to find the value of a for which the volume is maximum.
So, we know that we need to differentiate the volume with respect to a. Thus, we have
$\dfrac{dV}{da}=\dfrac{d}{da}\left( \dfrac{as-{{a}^{3}}}{4} \right)$
So, on differentiation, we get
$\dfrac{dV}{da}=\dfrac{d}{da}\left( \dfrac{as}{4} \right)-\dfrac{d}{da}\left( \dfrac{{{a}^{3}}}{4} \right)$
Hence, we now have the following equation
$\dfrac{dV}{da}=\dfrac{s}{4}-\dfrac{3{{a}^{2}}}{4}$
We now need to equate this differentiation with zero. So, we get
$\dfrac{s}{4}-\dfrac{3{{a}^{2}}}{4}=0$
Solving for a, we get
$3{{a}^{2}}=s$
Or, we can write
$a=\sqrt{\dfrac{s}{3}}$
We still need to see whether this is a maxima point or minima point.
So, ${{\left. \dfrac{{{d}^{2}}V}{d{{a}^{2}}} \right|}_{a=\sqrt{\dfrac{s}{3}}}}=\dfrac{d}{da}{{\left[ \dfrac{s}{4}-\dfrac{3{{a}^{2}}}{4} \right]}_{a=\sqrt{\dfrac{s}{3}}}}$
On solving this equation, we get
${{\left. \dfrac{{{d}^{2}}V}{d{{a}^{2}}} \right|}_{a=\sqrt{\dfrac{s}{3}}}}={{\left[ 0-\dfrac{3a}{2} \right]}_{a=\sqrt{\dfrac{s}{3}}}}$
On putting the value of a, we get
${{\left. \dfrac{{{d}^{2}}V}{d{{a}^{2}}} \right|}_{a=\sqrt{\dfrac{s}{3}}}}=\left[ -\dfrac{3\sqrt{\dfrac{s}{3}}}{2} \right]$
Or, we can write
${{\left. \dfrac{{{d}^{2}}V}{d{{a}^{2}}} \right|}_{a=\sqrt{\dfrac{s}{3}}}}=\left[ -\dfrac{\sqrt{3s}}{2} \right]$
We can clearly see that ${{\left. \dfrac{{{d}^{2}}V}{d{{a}^{2}}} \right|}_{a=\sqrt{\dfrac{s}{3}}}}<0$ .
Thus, the volume is maximum at $a=\sqrt{\dfrac{s}{3}}$ .
We know that the surface area is 27 $\text{i}{{\text{n}}^{2}}$ as is given in the question. So, we now get the value
$a=\sqrt{\dfrac{27}{3}}$
And since the value of a can never be negative, the value of a will be
$a=3$ .
Putting the values of a and s in equation (ii), we get
$V=\left( \dfrac{\left( 3\times 27 \right)-{{\left( 3 \right)}^{3}}}{4} \right)$
Thus, we get
$V=\left( \dfrac{\left( 3\times 27 \right)-27}{4} \right)$
On solving the above equation, we get
$V=\left( \dfrac{27}{2} \right)\text{i}{{\text{n}}^{3}}$
Hence, $V=13.5\text{ i}{{\text{n}}^{3}}$
Thus, the maximum volume of the open box is $13.5\text{ i}{{\text{n}}^{3}}$.

Note: We must remember that the surface area of open box with a square base is $s={{a}^{2}}+4ah$ and the surface area of a closed box with a square base is $s=2{{a}^{2}}+4ah$. Here, $a=\sqrt{\dfrac{s}{3}}$ , and since a can not be a negative value, we can say that $\sqrt{s}$ is also positive and thus, $\left[ -\dfrac{\sqrt{3s}}{2} \right]$ will be negative.