Question

Maximum velocity of the particle in SHM is $2cm/s$ then the magnitude of average velocity during one extreme position to another extreme position is
A.$\dfrac{\pi }{2}cm/s$
B.$\dfrac{\pi }{4}cm/s$
C.$\dfrac{4}{\pi }cm/s$
D.$\dfrac{2}{\pi }cm/s$

Answer 1

Hint: In this question, it is given that the particle is performing motion in Simple harmonic motion. Simple harmonic motion of an object or particle is a forth and back movement through its equilibrium position. By using the maximum velocity given the value of average velocity can be evaluated from one extreme position to another extreme position.
Formula used:
Maximum velocity formula
$ \Rightarrow {v_{\max }} = A\omega $
Average velocity formula
$ \Rightarrow {v_{avg}} = \dfrac{d}{t}$

Complete answer:
The position of a particle performing the simple harmonic motion can be given as a function of time
$ \Rightarrow x(t) = A\sin (\omega t)$ ------------- Equation $(1)$
Where $A = $Amplitude
$ \Rightarrow \omega = $Angular velocity
$ \Rightarrow t = $Time
Hence the velocity of the particle performing the simple harmonic motion can be obtained by differentiation of equation $(1)$
$ \Rightarrow \dfrac{d}{{dt}}x(t) = \dfrac{d}{{dt}}A\sin (\omega t)$
$ \Rightarrow v(t) = A\omega \cos (\omega t)$
$ \Rightarrow v(t) = {v_{\max }}\cos (\omega t)$
Now the maximum velocity can be given by
$ \Rightarrow {v_{\max }} = A\omega $ ------------ Equation $(2)$
Now as the particle is moving from one extreme point to another extreme point as from $A$ to $ - A$

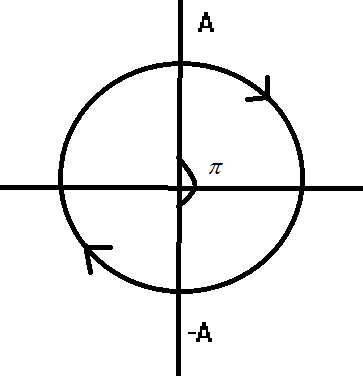
Now the total distance traveled would be given as $2A$ and the time is given as$t = \dfrac{T}{2}$, where $T$ is the time-period and average velocity ${v_{avg}}$ is given as the distance $d$ traveled per unit time $t$ is given as
$ \Rightarrow {v_{avg}} = \dfrac{d}{t}$
$ \Rightarrow {v_{avg}} = \dfrac{{2A}}{{T/2}}$
$ \Rightarrow {v_{avg}} = \dfrac{{4A}}{T}$ ---------- Equation $(3)$
Now as given maximum velocity is given as${v_{\max }} = 2cm/s$and also $\omega = \dfrac{{2\pi }}{T}$ . Substituting the value of angular velocity $\omega $in the equation $(2)$
$ \Rightarrow {v_{\max }} = \dfrac{{2\pi }}{T} \times A$
$ \Rightarrow 2cm/s = \dfrac{{2\pi }}{T} \times A$
$ \Rightarrow A = \dfrac{{2T}}{\pi }$ ---------- Equation $(4)$
Now substituting this value of equation $(4)$ in the equation $(3)$ we get
$ \Rightarrow {v_{avg}} = \dfrac{4}{T} \times \dfrac{{2T}}{\pi }$
$ \Rightarrow {v_{avg}} = \dfrac{2}{\pi }cm/s$
Therefore the magnitude of the average velocity from one extreme point to another extreme point is given $\dfrac{2}{\pi }cm/s$.

Hence option (D) is the right answer.

Note:
Simple harmonic is considered as a very good approximation. Some conditions should be fulfilled for an oscillation that follows simple harmonic motion. The two conditions are that acceleration should be proportional to the displacement from the mean position and it should be opposite to the direction of the displacement from the mean position.