Question

What is the maximum speed at which a railway carriage can move without toppling over along a curve of radius $R = 200m$if the distance from the centre of gravity of the carriage to the level of the rails is $h = 1.0m$, the distance between the rails is $h = 1.0m$, the distance between the rails is $l = 2.0m$and the rails are laid horizontally?(Take $g = 10m/{s^2}$)
A) $11.18m/s$
B) $22.36m/s$
C) $44.72m/s$
D) $74m/s$

Answer 1

Hint:In this question, we can solve the equations of translational equilibrium and rotational equilibrium which gives the relation between ${a_r}$ (rotational acceleration) and $g$ (gravitational acceleration). After that we can use the formula of rotational acceleration and find the maximum velocity of the railway carriage.

Complete step by step solution: -
In this question, we have a railway carriage which is moving in a curve of radius $R = 200m$. So, in the railway carriage’s frame, the carriage is in translational equilibrium as well as rotational equilibrium.

     

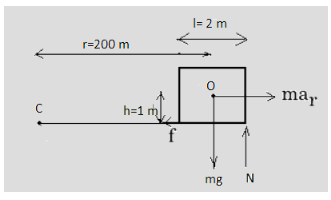
Now, for rotational equilibrium, the torque about the point \[O\] is zero i.e. ${\tau _0} = 0$
So, $f \times 1 - N \times 1 = 0$
$ \Rightarrow f = N$..................... (i)
Now, for translational equilibrium, we have-
$mg = N$
Substituting the value of $N$ from equation (i), we get-
$ \Rightarrow mg = f$.....................(ii)
Now, we know that force is the product of the mass and acceleration. So,
$f = m{a_r}$........................(iii)
Where \[m\] is the mass of the carriage and ${a_r}$ is the acceleration which is rotational acceleration (due to rotational motion)
Now, comparing equation (ii) and (iii), we get-
$
  m{a_r} = mg \\
   \Rightarrow {a_r} = g \\
$
Now, we know that ${a_r}$ is the rotational acceleration and is always equal to $\dfrac{{{v^2}}}{r}$. So, putting this value in the above equation, we get-
$
  \dfrac{{{v^2}}}{r} = g \\
   \Rightarrow {v^2} = rg \\
   \Rightarrow v = \sqrt {rg} \\
$
Now, from the question, we know that radius of the curve $r = 200m$ and gravitational acceleration $g = 10m/{s^2}$ , then the speed of the carriage is $v$. So,
$
  v = \sqrt {200 \times 10} \\
   \Rightarrow v = 44.72m/s \\
$
Hence, the maximum speed of the carriage is $44.72m/s$.

Therefore, option C is correct.

Note: - In this question, we have to keep in mind that there are two equilibriums- translational equilibrium and rotational equilibrium. We have to keep in mind that the carriage is having rotational motion so the acceleration used in $f = m{a_r}$ is rotational acceleration.