Question

What is the maximum length of the rod that can be placed inside a box having the shape of a cuboid of length 30cm, breadth 24cm and height 18cm?
A. \[30cm\]
B. \[30\sqrt 2 cm\]
C. \[24cm\]
D. \[18\sqrt 5 cm\]

Answer 1

Hint:
Here we have to find the maximum length of the rod that can be placed inside the box having cuboid shape. We need to know that the longest rod can be placed along the diagonal of the cuboid. We can find the maximum length by substituting the values of length, breadth, height in the formula of the length of diagonal of a cuboid.
Formula Used: Here we will use the formula \[{\text{Length of diagonal of a cuboid}} = \sqrt {{l^2} + {b^2} + {h^2}} \] , where \[l\] is the length of cuboid, \[b\] is the breadth of cuboid, \[h\] is the height of cuboid.

Complete step by step solution:
We will draw the diagram of the rod placed in the box.

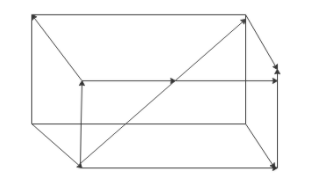
From the figure, we can say the longest rod that can be placed inside the cuboid box passes through the diagonal of the cuboid.
We can find the maximum length of the longest rod that can be placed inside the cuboid by using the formula length of diagonal of a cuboid.
We know that \[{\text{Length of diagonal of a cuboid}} = \sqrt {{l^2} + {b^2} + {h^2}} \].
We know that \[l = 30{\text{cm}}\], \[b = 24{\text{cm}}\] and \[h = 18{\text{cm}}\].
On substituting these values in formula, we get
\[\begin{array}{l}{\text{Length of diagonal of a cuboid}} = \sqrt {{{30}^2} + {{24}^2} + {{18}^2}} \\ = \sqrt {900 + 576 + 324} \\ = \sqrt {1800} \end{array}\]
Simplifying the above expression, we get
\[{\text{Length of diagonal of a cuboid}} = 30\sqrt 2 \]
Therefore, the maximum length of the rod is \[30\sqrt 2 cm\].

Hence, the correct option is option B.

Note:
Here we have considered the length of the rod is equal to the length of the diagonal of the cuboid because it was asked to find the maximum length. We will make a mistake if we consider the length of the rod is equal to the length of the cuboid. This will give the length of the rod but it will not be the maximum length.