Question

How do you maximize the volume of a right-circular cylinder that fits inside a sphere of radius $1$ m?

Answer 1

Hint: We have to maximize the volume of a right-circular cylinder that fits inside a sphere of radius $1$ m , its cross-sectional area and height are restricted by the sphere , we know that volume of a cylinder is given by $V = \pi {r^2}h$ . For maximum volume , $\dfrac{{dV}}{{dh}} = 0$ .

Complete step by step solution:
Consider a cylinder, however, is engraved in a sphere, its cross-sectional area and height are restricted by the sphere and when the sphere cut vertically then we get the required cross-section as shown below

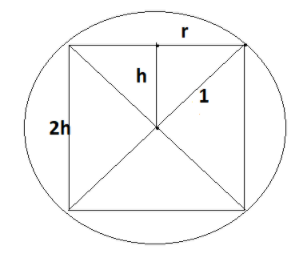
In the above figure ,
‘2h’ is the height of the cylinder ,
‘r’ is the radius of the cylinder,
And ‘1m’ is the radius of the sphere.
By applying Pythagoras Theorem , we will get the relationship between height of the cylinder, radius of the cylinder, radius of the sphere.
Therefore, we get the following,
$ \Rightarrow {1^2} = {h^2} + {r^2}$
Now, simplifying the above equation, we will get ,
$ \Rightarrow 1 = {h^2} + {r^2}$
For solving radius of the cylinder that is $r$, we will get ,
$ \Rightarrow {r^2} = 1 - {h^2}.......(1)$
Volume of a cylinder , $V = \pi {r^2}h$ . (original equation)
Now substitute $(1)$ in our original equation ,
We will get,
$V = \pi {r^2}h$
    $ = \pi \left( {1 - {h^2}} \right)2h$
    $ = \pi (h - {h^3})2$
For maximum volume , we can write ,
$ \Rightarrow \dfrac{{dV}}{{dh}} = 0$
$ \Rightarrow \dfrac{d}{{dh}}\left( {2\pi (h - {h^3})} \right) = 0$
$ \Rightarrow 2\pi (1 - 3({h^2})) = 0$
$ \Rightarrow (1 - 3{h^2}) = 0$
We have to solve for height of the cylinder that is $h$,
Subtract $1$ from both the side,
\[\begin{gathered}
   \Rightarrow 1 - 3({h^2}) = 0 \\
   \Rightarrow - 3{h^2} = - 1 \\
\end{gathered} \]
After simplifying ,
\[ \Rightarrow 3{h^2} = 1\]
Now multiple by $\dfrac{1}{3}$ both the side of the equation, we will get ,
\[ \Rightarrow {h^2} = \dfrac{1}{3}\]
Now, taking square root both the side,
$ \Rightarrow h = \sqrt {\dfrac{1}{3}} .......(2)$
Now, substitute $(1)$ and $(2)$in the original equation,
$V = \pi {r^2}h$
$ = \pi \left( {{1^2} - {h^2}} \right)2h$
$
   = \pi \left( {1 - \dfrac{1}{3}} \right)\dfrac{2}{{\sqrt 3 }} \\
   = \pi \left( {\dfrac{{3 - 1}}{3}} \right)\dfrac{2}{{\sqrt 3 }} \\
   = \dfrac{{4\pi }}{{3\sqrt 3 }} \\
$
We get the required result.

Hence the correct answer is $\dfrac{{4\pi }}{{3\sqrt 3 }}$

Note: The important thing to recollect when we have to maximize the volume of a right-circular cylinder that fits inside a sphere of constant radius, we have to derive the volume and then equate the result equals to zero.