
\[{\text{Maximise }}z{\text{ }} = {\text{ }}x{\text{ }} + {\text{ }}y,{\text{ subject to }}x{\text{ }} - {\text{ }}y{\text{ }} \leqslant {\text{ }} - 1,{\text{ }} - x{\text{ }} + {\text{ }}y{\text{ }} \leqslant {\text{ }}0,{\text{ }}x{\text{ }},{\text{ }}y{\text{ }} \geqslant {\text{ }}0\]
Answer
588k+ views
Hint: We can see all the points are present in a X-Y plane. We will plot, these points and mark the area:
For ‘≥’ sign area above the line whereas for ‘≤’ sign area below the line is considered.
To maximise the value, we need to consider the area lying above the same.
Complete step-by-step answer:
According to the question, we have to maximize \[z{\text{ }} = {\text{ }}x{\text{ }} + {\text{ }}y\]
Subjected to:
\[x{\text{ }} - {\text{ }}y{\text{ }} \leqslant {\text{ }} - 1\]
\[ - x{\text{ }} + {\text{ }}y{\text{ }} \leqslant {\text{ }}0\]
\[{\text{ }}x{\text{ }},{\text{ }}y{\text{ }} \geqslant {\text{ }}0\]
For finding the areas to be considered on the graph, we need to plot some points on the graph and these points can be calculated by equating either variable to 0:
For \[x{\text{ }} - {\text{ }}y{\text{ }} \leqslant {\text{ }} - 1:\]:
For \[ - x{\text{ + }}y{\text{ }} \leqslant {\text{ 0:}}\]:
Plotting these values on graph:
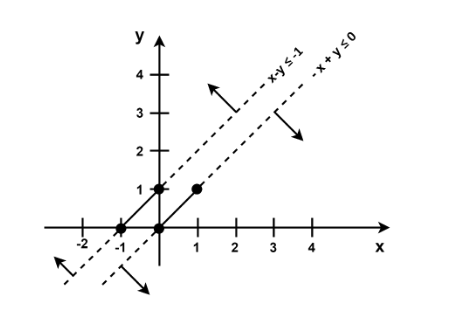
The arrows show the area that is to be considered by each line.
We can observe that there is no common or feasible region between the given lines.
This implies that there is no maximum value of Z.
Note: Feasible region is that region where all the points of subjects and constraints are satisfied.Be careful while taking the area into consideration based upon the signs of inequality present.Instead of colouring and shading the regions, draw arrows (as drawn in figure) for better clarification.
For ‘≥’ sign area above the line whereas for ‘≤’ sign area below the line is considered.
To maximise the value, we need to consider the area lying above the same.
Complete step-by-step answer:
According to the question, we have to maximize \[z{\text{ }} = {\text{ }}x{\text{ }} + {\text{ }}y\]
Subjected to:
\[x{\text{ }} - {\text{ }}y{\text{ }} \leqslant {\text{ }} - 1\]
\[ - x{\text{ }} + {\text{ }}y{\text{ }} \leqslant {\text{ }}0\]
\[{\text{ }}x{\text{ }},{\text{ }}y{\text{ }} \geqslant {\text{ }}0\]
For finding the areas to be considered on the graph, we need to plot some points on the graph and these points can be calculated by equating either variable to 0:
For \[x{\text{ }} - {\text{ }}y{\text{ }} \leqslant {\text{ }} - 1:\]:
| x | 0 | -1 |
| y | 1 | 0 |
For \[ - x{\text{ + }}y{\text{ }} \leqslant {\text{ 0:}}\]:
| x | 0 | 1 |
| y | 0 | 1 |
Plotting these values on graph:

The arrows show the area that is to be considered by each line.
We can observe that there is no common or feasible region between the given lines.
This implies that there is no maximum value of Z.
Note: Feasible region is that region where all the points of subjects and constraints are satisfied.Be careful while taking the area into consideration based upon the signs of inequality present.Instead of colouring and shading the regions, draw arrows (as drawn in figure) for better clarification.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





