
Match the table.
i. $\sigma_a$ m. $\dfrac{q_a + q_b}{4 \pi R^2}$ ii. $\sigma_b$ n. $\dfrac{-q_a }{4 \pi a^2}$ iii. $\sigma_R$ o. $\dfrac{ -q_b}{4 \pi b^2}$
A. (i, o), (ii, n), (iii, m)
B. (i, n), (ii, o), (iii, m)
C. (i, m), (ii, o), (iii, n)
D. (i, n), (ii, m), (iii, o)
| i. $\sigma_a$ | m. $\dfrac{q_a + q_b}{4 \pi R^2}$ |
| ii. $\sigma_b$ | n. $\dfrac{-q_a }{4 \pi a^2}$ |
| iii. $\sigma_R$ | o. $\dfrac{ -q_b}{4 \pi b^2}$ |
Answer
551.4k+ views
Hint: Surface charge density is the amount of charge present in per unit area of a surface. If we are given a spherical surface, then the amount of charge on its surface divided by the area of the sphere (depending on the radius) is the surface charge density.
Formula used:
For a spherical shell of radius r, the surface charge density is given as:
$\sigma = \dfrac{q}{A} = \dfrac{q}{4 \pi r^2}$
where q is the total charge on the entire spherical surface.
Complete step by step answer:
For a thin sheet, positively charged with charge q and of area A, the surface charge density is simply, $\sigma = q/A$
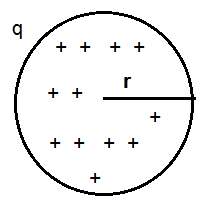
The surface charge density for a spherical surface with same charge will become:
$\sigma = \dfrac{q}{A} = \dfrac{q}{4 \pi r^2}$
If we look closely we will observe that the left hand side column has all surface charge densities with the radius of respective surface (spherical) as subscript. On the right hand side column, we have the values for different surface charge density that are given a jumbled order. We know that surface charge density is the ratio of total charge on the surface by total area of the surface. In the three options in the right hand side column, if we go by total charge then we can observe that it is not clear information to mark distinct surface charge densities as two different surfaces (with different radii) can have the same amount of charge on them. In that case, the density of the surface with a bigger radius will be less. Therefore we differentiate among all three options based on their radii. So, we can conclude that in the right hand side column m has R as the radius so it must signify density $\sigma_R$ given as option (iii) on the RHS column. Similarly, n has a radius a corresponding to density $\sigma_a$ in option (i) and o has radius b so corresponding density is $\sigma_b$ in option (ii).
Therefore, from the given set of options, the one that matches correctly the two columns is option (B).
Note:
This question might appear to be a little confusing because of the total charges that have been placed in the numerator in the right hand side column. To sort this out one can think of a situation when we impart some charge to a spherical surface and place another spherical surface near it. On the surface of the second sphere, equal and opposite charge develops (or gets induced). In magnitude the two spheres would now have equal charges but the densities of the two will differ due to their radii.
Formula used:
For a spherical shell of radius r, the surface charge density is given as:
$\sigma = \dfrac{q}{A} = \dfrac{q}{4 \pi r^2}$
where q is the total charge on the entire spherical surface.
Complete step by step answer:
For a thin sheet, positively charged with charge q and of area A, the surface charge density is simply, $\sigma = q/A$

The surface charge density for a spherical surface with same charge will become:
$\sigma = \dfrac{q}{A} = \dfrac{q}{4 \pi r^2}$

If we look closely we will observe that the left hand side column has all surface charge densities with the radius of respective surface (spherical) as subscript. On the right hand side column, we have the values for different surface charge density that are given a jumbled order. We know that surface charge density is the ratio of total charge on the surface by total area of the surface. In the three options in the right hand side column, if we go by total charge then we can observe that it is not clear information to mark distinct surface charge densities as two different surfaces (with different radii) can have the same amount of charge on them. In that case, the density of the surface with a bigger radius will be less. Therefore we differentiate among all three options based on their radii. So, we can conclude that in the right hand side column m has R as the radius so it must signify density $\sigma_R$ given as option (iii) on the RHS column. Similarly, n has a radius a corresponding to density $\sigma_a$ in option (i) and o has radius b so corresponding density is $\sigma_b$ in option (ii).
Therefore, from the given set of options, the one that matches correctly the two columns is option (B).
Note:
This question might appear to be a little confusing because of the total charges that have been placed in the numerator in the right hand side column. To sort this out one can think of a situation when we impart some charge to a spherical surface and place another spherical surface near it. On the surface of the second sphere, equal and opposite charge develops (or gets induced). In magnitude the two spheres would now have equal charges but the densities of the two will differ due to their radii.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




