Question

Match the column I with column II

Answer 1

Hint: In this question, we will use the expression which gives relation between time, mass and the spring constant. We will also use the expression for effective spring constant in both series and parallel. These expressions will help us to match the two columns. Further, we will study about the SHM produced by a spring attached with a block, for better understanding.

Formula used:
$T = 2\pi \sqrt {\dfrac{m}{{{K_{eff}}}}} $

Complete step by step solution:
As we know, time period of spring block system is given as:
$T = 2\pi \sqrt {\dfrac{m}{{{K_{eff}}}}} ...........(1)$

As we know that in series Keff is given by:
${K_{eff}} = \dfrac{1}{{{K_1}}} + \dfrac{1}{{{K_2}}} = \dfrac{{{K_1} + {K_2}}}{{{K_1}{K_2}}}.........(2)$

Also, in parallel Keff is given by:
${K_{eff}} = {K_1} + {K_2}............(3)$
 
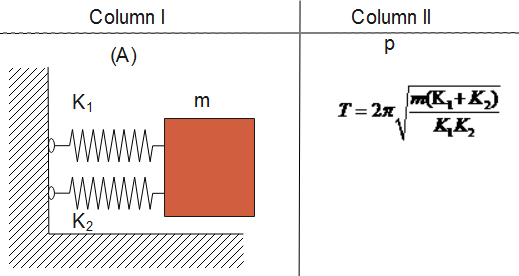
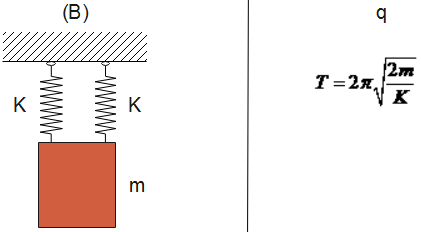
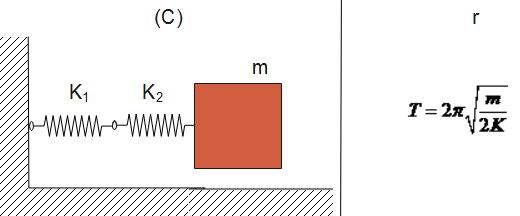
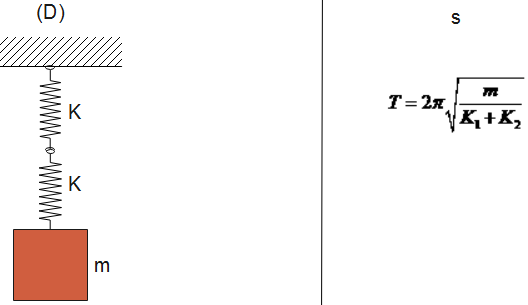
Now, when we see in the given diagram (A) and (B) springs are connected in parallel, whereas in diagram (C) and (D), the spring is connected in series.

So, from the above equations (1), (2) and (3) we will match the following as:
A-s, B-r, C-p, D-q
Therefore we got the required answer.

Additional information:
As we know that a simple harmonic motion is defined as a special type of periodic motion where the restoring force on the moving object is directly proportional to the magnitude of displacement of the object and therefore it acts upon the object's equilibrium position.
Further, we know that the frequency or the time period of a simple harmonic motion depends on variable forces and it does not depend on the constant external force. Further, this constant external force can only change the mean position of the wooden block.
Here, the mean position is at the natural length of the spring in the absence of an electric field, whereas when the electric field is present the mean position of the string will be obtained after a compression.
So, the simple harmonic motion or SHM of the wooden block will be of the same frequency and with shifted mean position.

Note:
We should remember that the force required to stretch a metal spring is directly proportional to the extension of that spring. This law is known as Hooke's law. We should note that this question could be easily solved if we know the basic formula of K effective in both series and parallel.