Question

Mark the position of the revolving line when ${{420}^{g}}$ it has traced out the following angles.
A. ${{420}^{g}}$
B. ${{875}^{g}}$

Answer 1

Hint: To solve this question, we have to convert the angles into degrees if they are not given in degrees by using the relation between radian and degrees, which is, $\text{Degree}=\text{Gradian}\times 0.9$. Then we will try to write the given angle in the form of $n\pi +\theta $, and then we will be able to trace the line on a 2D graph on which the positive x axis represents even $\pi $ angles and negative y axis represents odd $\pi $ angles.

Complete step-by-step answer:
In this question, we have been asked to trace the position of the revolving line of some angles. For that, we will first convert the angles into degrees by using the relation, $\text{Degree}=\text{Gradian}\times 0.9$ and then convert the degrees into radians to express it in the form of $n\pi +\theta $, where n is a natural number. So, let us consider each part of the question individually.
A. ${{420}^{g}}$
Here we have angels in the gradian form, and so we have to convert it into radians. So, we will first convert it into degrees. We know that, $\text{Degree}=\text{Gradian}\times 0.9$. So, we can write as,
$\begin{align}
  & {{420}^{g}}\text{ in degrees}=420\times 0.9 \\
 & \Rightarrow {{420}^{g}}\text{ in degrees}=378{}^\circ \\
\end{align}$
Now, we will convert $378{}^\circ $ into radians to express that in $n\pi +\theta $ form. We know that $180{}^\circ =\pi \text{ }radians$, and therefore we can write it as, $1{}^\circ =\dfrac{\pi }{180}radians$. So, we will get,
$\begin{align}
  & 378{}^\circ =378\times \dfrac{\pi }{180}radians \\
 & \Rightarrow 378{}^\circ =\dfrac{21\pi }{10}radians \\
\end{align}$
Now, we will express $\dfrac{21\pi }{10}$ in terms of $n\pi +\theta $. And so, we will write the same as,
$\begin{align}
  & \dfrac{21\pi }{10}=\dfrac{20\pi +\pi }{10} \\
 & \Rightarrow \dfrac{21\pi }{10}=2\pi +\dfrac{\pi }{10} \\
\end{align}$
Now, we can say that ${{420}^{g}}=2\pi +\dfrac{\pi }{10}radians$. Now, for tracing the line, we know that one revolution is completed when angle is $2\pi $, so here one complete revolution has been completed by the line. Then, we can see that it will either lie in the first quadrant or in the second quadrant, depending on $\dfrac{\pi }{10}$, which cannot be expressed as the sum of some angles with $\dfrac{\pi }{2}$. So, it will lie in the first quadrant at an angle of $\dfrac{\pi }{10}$ from the positive x axis. Hence, we can represent the line as line OA as in the figure given below.

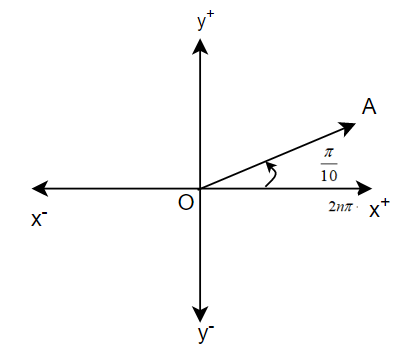
B. ${{875}^{g}}$
Here, we can see that we have been given an angle in the gradient, so we have to convert it into radians. For that we will first convert it into degrees. We know that, $\text{Degree}=\text{Gradian}\times 0.9$. So, we can write as,
$\begin{align}
  & {{875}^{g}}\text{ in degrees}=875\times 0.9 \\
 & \Rightarrow {{875}^{g}}\text{ in degrees}=787.5{}^\circ \\
\end{align}$
Now, we will convert $787.5{}^\circ $ into radians in order to express the same in $n\pi +\theta $ form. We know that $180{}^\circ =\pi \text{ }radians$, and so, we can write it as, $1{}^\circ =\dfrac{\pi }{180}radians$. Hence, we will write,
$\begin{align}
  & 787.5{}^\circ =787.5\times \dfrac{\pi }{180}\text{ }radians \\
 & \Rightarrow 787.5{}^\circ =\dfrac{35\pi }{8}\text{ }radians \\
\end{align}$
Now, we will express $\dfrac{35\pi }{8}$ in terms of $n\pi +\theta $. So, for that, we will write the same as,
$\begin{align}
  & \dfrac{35\pi }{8}=\dfrac{32\pi +3\pi }{8} \\
 & \Rightarrow \dfrac{35\pi }{8}=4\pi +\dfrac{3\pi }{8}=2\times 2\pi +\dfrac{3\pi }{8} \\
\end{align}$
Now, we can say that ${{875}^{g}}=4\pi +\dfrac{3\pi }{8}radians$. We know that one revolution is completed when angle is $2\pi $, so here 2 complete revolutions have been completed by the line. Now, for tracing the line, we can see that it will either lie in the first quadrant or in the second quadrant, depending on the value of $\dfrac{3\pi }{8}$. We cannot represent it in the form of $\dfrac{\pi }{2}+\theta $, so it will lie in the first quadrant at an angle of $\dfrac{3\pi }{8}$ from the positive x axis. Hence, we can represent the line as line OB as in the figure given below.

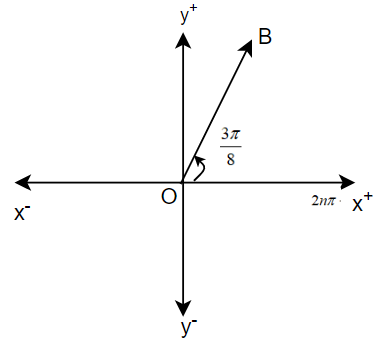
Note: Here, we have expressed the angles in the form of $n\pi +\theta $, because in coordinate axis we have four quadrants and after angle of $360{}^\circ =2\pi $, we will again reach the first quadrant and then the angles start repeating. Also, while converting degrees into radian, we need to remember that $\pi \text{ }radians=180{}^\circ $. If we make any silly mistake while writing the angles, we will get a different quadrant and also our figure will change completely, so we must be careful.