Question

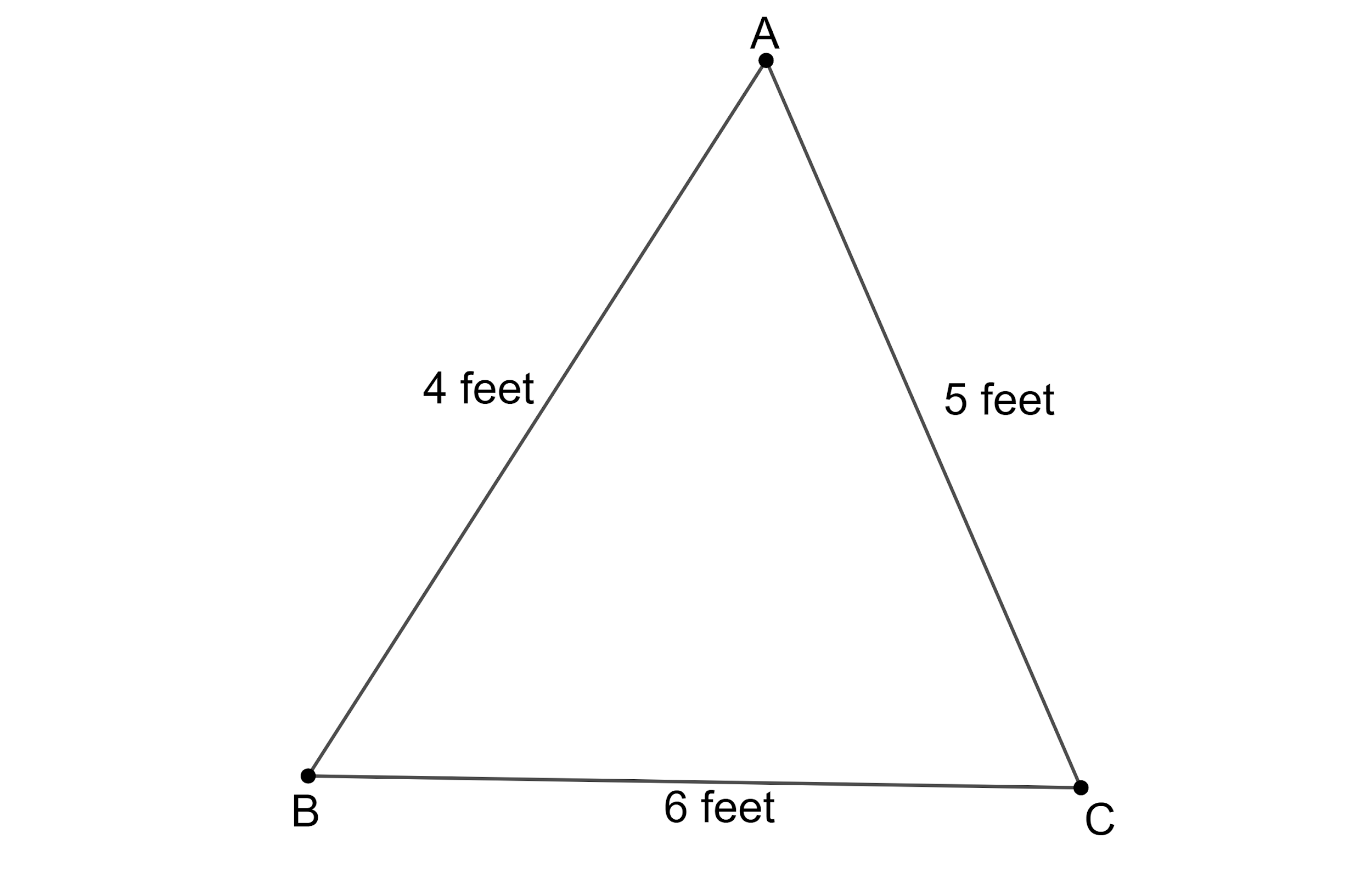
Manu has decided to create a triangular flower bed border. He plans to use 3 pieces of rectangular wooden plates with lengths 4, 5 and 6 feet, as shown in figure. Manu plans to cut the 3 pieces of plate for the flower bed border from a single piece of plate. If $\dfrac{1}{8}$ inch wood is wasted in every cut, calculate the shortest single piece of plate which can be used by Manu (in inches)?

(a) 178
(b) 179
(c) 180
(d) 181
(e) 182

Answer 1

Hint: We start solving the problem by assigning the variable for the required length of the single piece of plate. We then find the total amount wasted due to cutting of this piece of plate. We then add the sides of the triangle and wasted length by using the fact that 1 foot = 12 inches to get the required length in inches. We then find the nearest greater value of the obtained value to get the required answer.

Complete step-by-step answer:
According to the problem, we are given that the triangular flower bed border is made of three rectangular plate pieces of lengths 4, 5 and 6 feet. We need to find the length of the shortest single piece of plate which can be used to make a triangular flower bed border if $\dfrac{1}{8}$ inch wood is wasted in every cut.
Let us re draw the given triangular flower bed border.

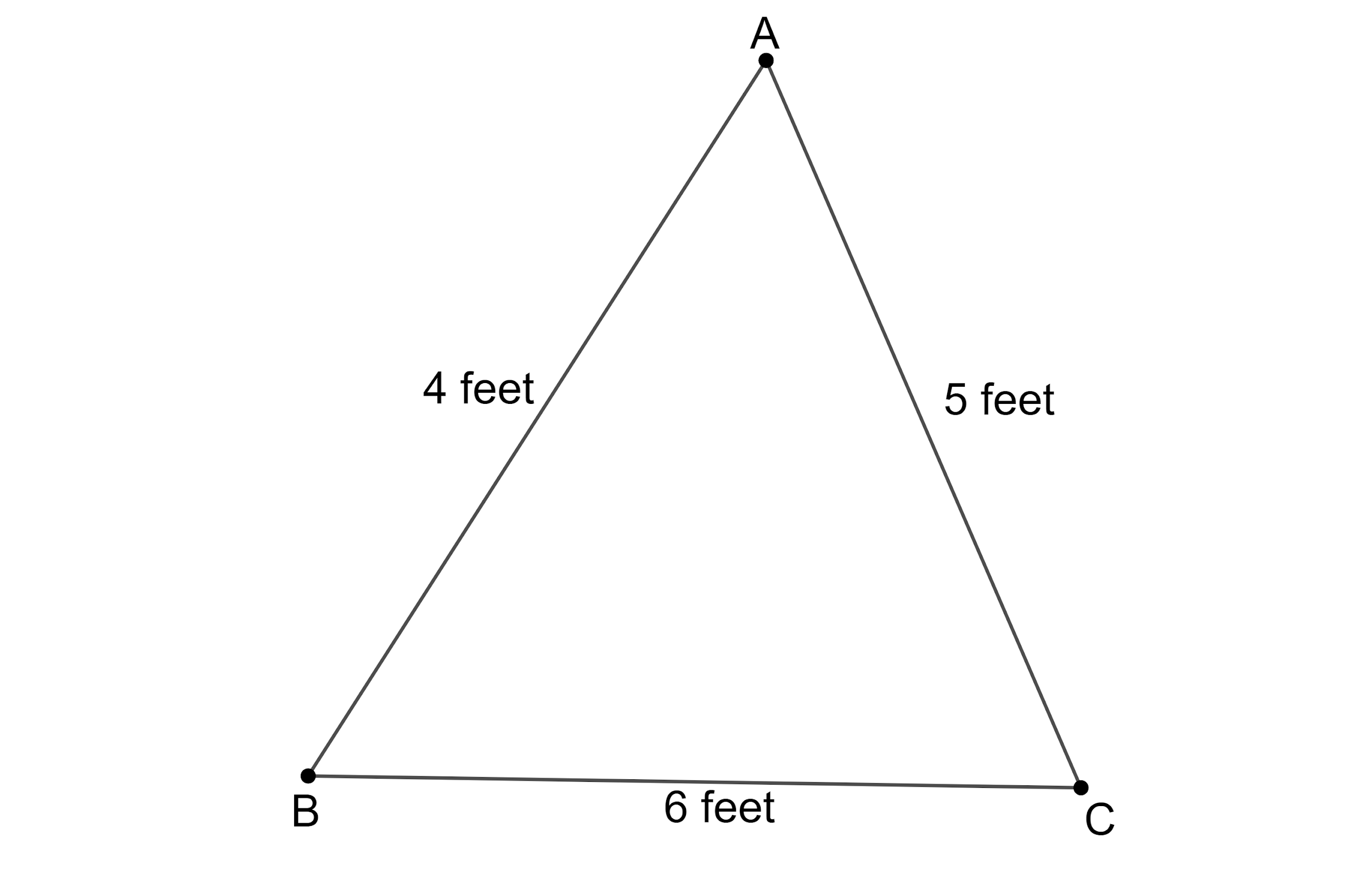
Let us assume the length of the single piece of rectangular plate to be ‘x’ inches.
We know that the sides are cut from these ‘x’ inches. We need to cut two times to this single piece in order to get the 3 rectangular plates for the triangular bed border.
So, the total length of the plate wasted = $2\times \dfrac{1}{8}=\dfrac{1}{4}$ inches.
We know that 1 foot = 12 inches.
So, the length of the single piece of rectangular plate(x) = AB + BC + CA + wasted length.
$\Rightarrow x=\left( 4\times 12 \right)+\left( 6\times 12 \right)+\left( 5\times 12 \right)+\dfrac{1}{4}$ inches.
$\Rightarrow x=48+72+60+0.25$ inches.
$\Rightarrow x=180.25$ inches.
Let us find the nearby integer which is greater than 180.25 inches, which is 181inches.
So, we have found the shortest single piece of plate which can be used by Manu as 181 inches.

So, the correct answer is “Option d”.

Note: Here we assume that the required plate is rectangle in shape and single cuts are to be made to get the required sides of the triangle. We should not make calculation mistakes while solving this problem. We can also find the area of the triangular bed border using the length of the sides given. Similarly, we can expect problems to find the angles present in the triangular bed border.