
How do you make the graph for $y=\ln \left( 1+\dfrac{x}{\ln \left( 1-x \right)} \right)$?
Answer
561.3k+ views
Hint: We recall the domain and range of natural logarithmic function. We use restriction of domain on the natural logarithmic function to find restriction on the argument $1+\dfrac{x}{\ln \left( 1-x \right)}$. We use these restrictions to plot a decreasing curve within interval $x\in \left( 0,1 \right]$with asymptotes as negative $y-$axis.
Complete step by step answer:
We know that natural logarithmic function which has base $e$ only takes positive real values as inputs or arguments. It means
\[\ln x:{{\mathsf{\mathbb{R}}}^{+}}\to \mathsf{\mathbb{R}}\]
We also know $\ln x$ returns positive value if $x > 1$ which means $\ln x > 0\Rightarrow x > 1$. The function $\ln x$ returns negative if $x\in \left( 0,1 \right)$ which means$\ln x < 0\Rightarrow x\in \left( 0,1 \right)$. The zero for $\ln x$ is $x=1$ which means $\ln x=0\Rightarrow x=1$ \[\]
We are asked to find the graph of following function
\[y=\ln \left( 1+\dfrac{x}{\ln \left( 1-x \right)} \right)\]
We see that the logarithm inside the bracket $\ln \left( 1-x \right)$ exists if $1-x > 0\Rightarrow x < 1$. We also have
\[\begin{align}
& 1+\dfrac{x}{\ln \left( 1-x \right)} > 0 \\
& \Rightarrow t > 0\left( \text{where }1+\dfrac{x}{\ln \left( 1-x \right)}=t\text{ } \right) \\
\end{align}\]
Now we get 3 possible cases. \[\]
Case-1:We first have the denominator $\ln \left( 1-x \right) > 0$ then we have
\[\begin{align}
& 1-x > 1 \\
& \Rightarrow -x > 0 \\
& \Rightarrow x < 0 \\
\end{align}\]
We use the above result $x < 0$ and $\ln \left( 1-x \right) > 0$ to check that $1+\dfrac{x}{\ln \left( 1-x \right)} < 1$ . So we cannot have $\ln \left( t \right) > 0$ from case-1. \[\]
Case-2:We have
\[\begin{align}
& \ln \left( 1-x \right)=0 \\
& \Rightarrow 1-x=1 \\
& \Rightarrow x=0 \\
\end{align}\]
We use L’hospital rule to on the argument of $t$ t have
\[\begin{align}
& \displaystyle \lim_{x \to 0}t=\displaystyle \lim_{x \to 0}\left( 1+\dfrac{x}{\ln \left( 1-x \right)} \right) \\
& \Rightarrow \displaystyle \lim_{x \to 0}t=1+\displaystyle \lim_{x \to 0}\dfrac{x}{\ln \left( 1-x \right)} \\
& \Rightarrow \displaystyle \lim_{x \to 0}t=1+\displaystyle \lim_{x \to 0}\dfrac{1}{\dfrac{1}{1-x}\left( -1 \right)} \\
& \Rightarrow \displaystyle \lim_{x \to 0}t=1-1=0 \\
\end{align}\]
So we argue that $t$ approaches to 0 as $x$ approaches to 0. \[\]
Case-3: We have
\[\begin{align}
& \ln \left( 1-x \right) > 0 \\
& \Rightarrow 1-x > 1 \\
& \Rightarrow -x > 0 \\
& \Rightarrow x < 0 \\
\end{align}\]
We use the above result $x < 0$ and previously obtained $\ln \left( 1-x \right) > 0$ to check that $1+\dfrac{x}{\ln \left( 1-x \right)} > 1\Rightarrow t > 1$ . So we cannot have $\ln \left( t \right) > 0$ from case-3. So our function is valid for $x\in \left( 0,1 \right)$ and as $x \to 1$ we have $y=\ln t\to 1$. We also have $x \to 0\Rightarrow y\to -\infty $.So our required graph is \[\]
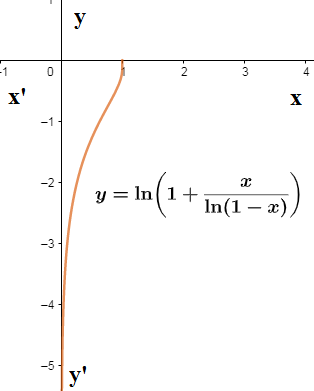
Note:
We note that the given graph is the graph of a decreasing curve starting from $x=1$ and asymptotic about the negative $y-$ axis which means the curve meets the $y-$ axis at infinity. We note that if there two functions $f\left( x \right),g\left( x \right)$ such that $f\left( x \right)\to 0,g\left( x \right)\to 0$ as $x \to 0$ then we have the quotient $\dfrac{f\left( x \right)}{g\left( x \right)}$ in $\dfrac{0}{0}$ indeterminate from. We find the quotients in indeterminate from using L’hospital rule as $\displaystyle \lim_{x \to 0}\dfrac{f\left( x \right)}{g\left( x \right)}=\dfrac{{{f}^{'}}\left( x \right)}{{{g}^{'}}\left( x \right)}$. The other indeterminate form is $\dfrac{\infty }{\infty },{{1}^{\infty }},\infty -\infty $ etc.
Complete step by step answer:
We know that natural logarithmic function which has base $e$ only takes positive real values as inputs or arguments. It means
\[\ln x:{{\mathsf{\mathbb{R}}}^{+}}\to \mathsf{\mathbb{R}}\]
We also know $\ln x$ returns positive value if $x > 1$ which means $\ln x > 0\Rightarrow x > 1$. The function $\ln x$ returns negative if $x\in \left( 0,1 \right)$ which means$\ln x < 0\Rightarrow x\in \left( 0,1 \right)$. The zero for $\ln x$ is $x=1$ which means $\ln x=0\Rightarrow x=1$ \[\]
We are asked to find the graph of following function
\[y=\ln \left( 1+\dfrac{x}{\ln \left( 1-x \right)} \right)\]
We see that the logarithm inside the bracket $\ln \left( 1-x \right)$ exists if $1-x > 0\Rightarrow x < 1$. We also have
\[\begin{align}
& 1+\dfrac{x}{\ln \left( 1-x \right)} > 0 \\
& \Rightarrow t > 0\left( \text{where }1+\dfrac{x}{\ln \left( 1-x \right)}=t\text{ } \right) \\
\end{align}\]
Now we get 3 possible cases. \[\]
Case-1:We first have the denominator $\ln \left( 1-x \right) > 0$ then we have
\[\begin{align}
& 1-x > 1 \\
& \Rightarrow -x > 0 \\
& \Rightarrow x < 0 \\
\end{align}\]
We use the above result $x < 0$ and $\ln \left( 1-x \right) > 0$ to check that $1+\dfrac{x}{\ln \left( 1-x \right)} < 1$ . So we cannot have $\ln \left( t \right) > 0$ from case-1. \[\]
Case-2:We have
\[\begin{align}
& \ln \left( 1-x \right)=0 \\
& \Rightarrow 1-x=1 \\
& \Rightarrow x=0 \\
\end{align}\]
We use L’hospital rule to on the argument of $t$ t have
\[\begin{align}
& \displaystyle \lim_{x \to 0}t=\displaystyle \lim_{x \to 0}\left( 1+\dfrac{x}{\ln \left( 1-x \right)} \right) \\
& \Rightarrow \displaystyle \lim_{x \to 0}t=1+\displaystyle \lim_{x \to 0}\dfrac{x}{\ln \left( 1-x \right)} \\
& \Rightarrow \displaystyle \lim_{x \to 0}t=1+\displaystyle \lim_{x \to 0}\dfrac{1}{\dfrac{1}{1-x}\left( -1 \right)} \\
& \Rightarrow \displaystyle \lim_{x \to 0}t=1-1=0 \\
\end{align}\]
So we argue that $t$ approaches to 0 as $x$ approaches to 0. \[\]
Case-3: We have
\[\begin{align}
& \ln \left( 1-x \right) > 0 \\
& \Rightarrow 1-x > 1 \\
& \Rightarrow -x > 0 \\
& \Rightarrow x < 0 \\
\end{align}\]
We use the above result $x < 0$ and previously obtained $\ln \left( 1-x \right) > 0$ to check that $1+\dfrac{x}{\ln \left( 1-x \right)} > 1\Rightarrow t > 1$ . So we cannot have $\ln \left( t \right) > 0$ from case-3. So our function is valid for $x\in \left( 0,1 \right)$ and as $x \to 1$ we have $y=\ln t\to 1$. We also have $x \to 0\Rightarrow y\to -\infty $.So our required graph is \[\]
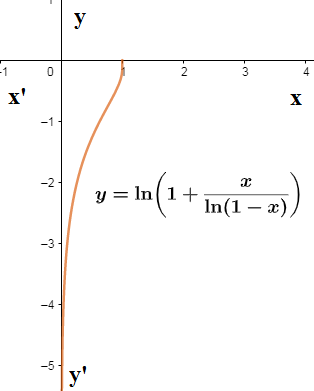
Note:
We note that the given graph is the graph of a decreasing curve starting from $x=1$ and asymptotic about the negative $y-$ axis which means the curve meets the $y-$ axis at infinity. We note that if there two functions $f\left( x \right),g\left( x \right)$ such that $f\left( x \right)\to 0,g\left( x \right)\to 0$ as $x \to 0$ then we have the quotient $\dfrac{f\left( x \right)}{g\left( x \right)}$ in $\dfrac{0}{0}$ indeterminate from. We find the quotients in indeterminate from using L’hospital rule as $\displaystyle \lim_{x \to 0}\dfrac{f\left( x \right)}{g\left( x \right)}=\dfrac{{{f}^{'}}\left( x \right)}{{{g}^{'}}\left( x \right)}$. The other indeterminate form is $\dfrac{\infty }{\infty },{{1}^{\infty }},\infty -\infty $ etc.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




