Question

What is the magnitude of angular velocity of the stick plus puck after the collision?

Answer 1

Hint: Apply the law of conservation of angular momentum to calculate the final angular velocity of the stick plus puck system. It states that the total angular momentum of a system about a fixed point is constant as long as there is no external torque acting on it. The center of mass of system of two particles is ${r_{cm}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}}$. Here, ${r_1}$ and ${r_2}$ are the distance of the masses ${m_1}$ and ${m_2}$ from the origin of the frame of reference.

Complete step by step answer:
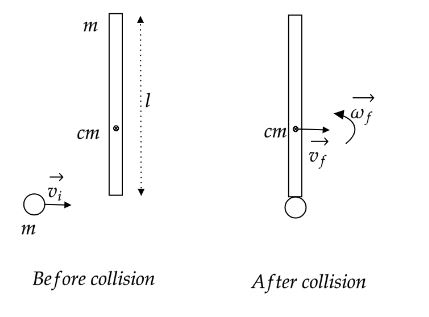
It is given that the length of the stick is $l$. The stick and the puck have the same mass $m$.Before the collision, the stick at rest and the puck travels with initial velocity ${\vec v_i}$. The center of mass of the stick will be at the center of the stick i.e., at $\dfrac{l}{2}$ w.r.t. to the top of the stick. The puck strikes at the end of the stick. The puck and the stick will form a new system. The distance of the puck w.r.t. the top of the stick is $l$. The new center of mass of the system w.r.t the top of the stick is given by,
${r_{cm}} = \dfrac{{{m_{puck}} \cdot l + {m_{stick}} \cdot \dfrac{l}{2}}}{{{m_{puck}} + {m_{stick}}}}$

Substitute ${m_{puck}} = {m_{stick}} = m$ and then simplify the above equation.
$ \Rightarrow {r_{cm}} = \dfrac{3}{4}l$
Just before the collision, the angular momentum of the stick is zero i.e., ${L_{i,stick}} = 0$.
The distance of the puck w.r.t. the center of mass of the system is,
${r_{puck}} = \left( {l - \dfrac{3}{4}l} \right) = \dfrac{l}{4}$
Just before the collision, the angular momentum of the puck is,
${L_{i,puck}} = m{v_i}\left( {\dfrac{l}{4}} \right)$
The total angular momentum of the system before the collision is;
${L_i} = {L_{i,puck}} + {L_{i,stick}}$
$ \Rightarrow {L_i} = \dfrac{{m{v_i}l}}{4} + 0$
$\Rightarrow{L_i} = \dfrac{{m{v_i}l}}{4}$

After the collision, the system has a rotational motion about its center of mass.Let the final angular velocity of the system after the collision is ${\overrightarrow \omega _f}$ .After the collision, the final angular momentum of the system is given by
${L_f} = I{\omega _f}$
Where, $I$ is the moment of inertia of the system after the collision.
$I = {I_{stick}} + {I_{puck}}$
${I_{puck}}$ is the moment of inertia of the puck after the collision.
${I_{puck}} = m{r_{puck}}^2$
Substitute ${r_{puck}} = \dfrac{l}{4}$ in the above formula. We got
${I_{puck}} = \dfrac{{m{l^2}}}{{16}}$
${I_{stick}}$ is the moment of inertia of the stick about the center of mass of the system after the collision.

Apply the parallel axis theorem to calculate the ${I_{stick}}$.
${I_{stick}} = {I_{cm,stick}} + m{r^2}$
Where, ${I_{cm,stick}}$ is the moment of inertia of the stick about its center of mass.
${I_{sm,stick}} = \dfrac{1}{{12}}m{l^2}$
$r$ is the distance of the center of mass of the stick from the center of mass of the system.
$r = \dfrac{{3l}}{4} - \dfrac{l}{2}$
$ \Rightarrow r = \dfrac{l}{4}$
Substitute the values of $r$ and ${I_{cm,stick}}$ in the above formula for ${I_{stick}}$.
${I_{stick}} = \dfrac{1}{{12}}m{l^2} + m{\left( {\dfrac{l}{4}} \right)^2}$
Now the total moment of inertia becomes
$I = {I_{stick}} + {I_{puck}}$
$ \Rightarrow I = \dfrac{1}{{12}}m{l^2} + m{\left( {\dfrac{l}{4}} \right)^2} + \dfrac{{m{l^2}}}{{16}}$

Further simplifying, we got
$ \Rightarrow I = \dfrac{5}{{24}}m{l^2}$
Now as per the conservation of angular momentum, ${L_i} = {L_f}$.
$ \Rightarrow m{v_i}\left( {\dfrac{l}{4}} \right) = I{\omega _f}$
$ \Rightarrow {\omega _f} = \dfrac{{\dfrac{{m{v_i}l}}{4}}}{I}$
Substitute the value of $I$ in the above equation.
$ \Rightarrow {\omega _f} = \dfrac{{\dfrac{{m{v_i}l}}{4}}}{{\dfrac{5}{{24}}m{l^2}}}$
Further simplifying, we got
$ \therefore {\omega _f} = \dfrac{{6{v_i}}}{{5l}}$

Hence, the final angular velocity of the stick pus puck system is ${\omega _f} = \dfrac{{6{v_i}}}{{5l}}$.

Note: It should be noted that the moment of inertia of a rod about its center of mass is $I = \dfrac{1}{{12}}M{R^2}$. Where, $M$ and $R$ are the mass and length of the rod.The parallel axis theorem states that the moment of inertia $\left( I \right)$ of a system about an axis parallel to an axis passing through its center of mass is equal to the sum of the moment of inertia $\left( {{I_{cm}}} \right)$ of the system about the axis passing through its center of mass and the product of mass $\left( M \right)$ of the system and the distance $\left( R \right)$ between the two axes.
$I = {I_{cm}} + M{R^2}$.