Question

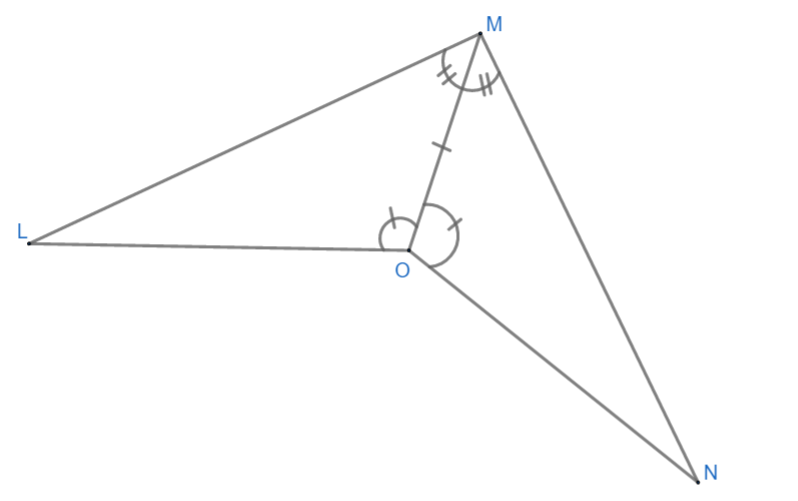
Looking at the figure, which method you would use to prove $ \Delta OML\cong \Delta OMN $ and ML = MN if OM bisects $ \angle LMN\text{ and }\angle LON $ .

A. SAS congruence theorem.
B. CPCT
C. AAA congruence theorem.
D. SSS congruence theorem.

Answer 1

Hint: In this question, we are given two triangles where both triangles are congruent and we need to tell the rule by which the triangles are congruent and sides are equal. For this, we will understand various congruence conditions and then compare them with given triangles to find our required answer.

Complete step by step solution:
Let us first understand different congruence conditions for the two triangles.
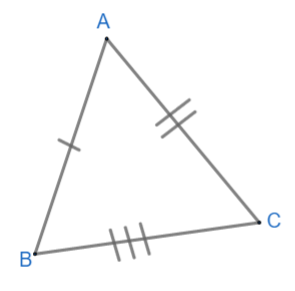
SSS congruence rule: All three sides of a triangle are equal to the corresponding sides of another triangle, then triangles are congruent with the SSS rule of congruence. Example, $ \Delta ABC\text{ and }\Delta PQR $ are congruent because AB = PQ, BC = QR and AC = PR.

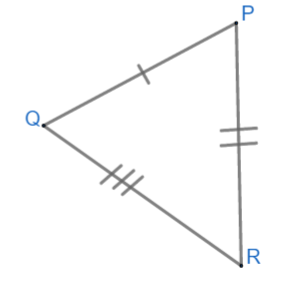
SAS congruence rule: If any two sides of a triangle are equal to the corresponding sides of the other triangle. Also, the angle between sides of both triangles are also equal then triangles are congruent. Example, $ \Delta ABC\text{ and }\Delta PQR $ are congruent because AB = PQ, AC = PR and $ \angle A=\angle P $ .

AAA: There is not AAA congruence rule but AAA is the similarity rule where all corresponding angles are equal.
CPCT refers to the rule stating that the corresponding part of congruent triangles is equal.
Now, look at a given diagram.

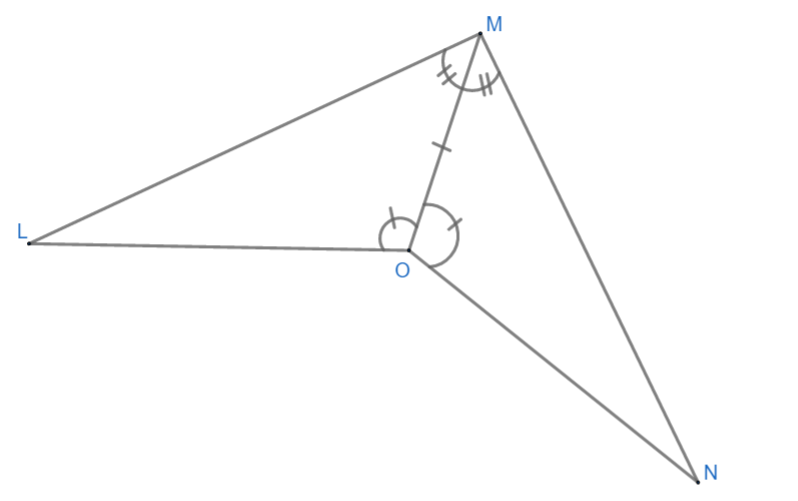
Here in $ \Delta MOL\text{ and }\Delta MON $ we have,
(I) $ \angle MOL=\angle MON $ because OH bisects $ \angle LON $ .
(II) $ \angle OML=\angle OMN $ because OM bisects $ \angle LMN $ .
(III) OM = OM because it is the common side in both triangles.
By comparing with discussed rules, we see that all rules match with SAS congruence rule.
Therefore, $ \angle MOL\cong \angle MON $ by SAS congruence rule. So option A is the correct for $ \angle MOL\cong \angle MON $.
For ML = MN we can apply CPCT because given triangles are congruent.
So option B is correct for ML = MN.

Note:
 Students should note the difference between SAS and SSA congruence rule. In SAS, the angle is between the side which is equal to other triangles’ corresponding sides whereas, in SSA, any of the angles can be equal to the corresponding angle of other triangles. There is one more congruence rule which is the RHS congruence rule.