Question

How much longer is $1$ inch button than an $\dfrac{3}{8}$ inch button?

Answer 1

Hint: Firstly, take both the quantities and compare which is larger. Then write them in a subtraction equation and evaluate using the LCM method or else by cross-multiplying the fractions and then subtracting the second number from the first to get the numerator part and multiply the denominators to get a common denominator.

Complete step-by-step answer:
Given quantities are, $1$ inch and $\dfrac{3}{8}$ inch.
       

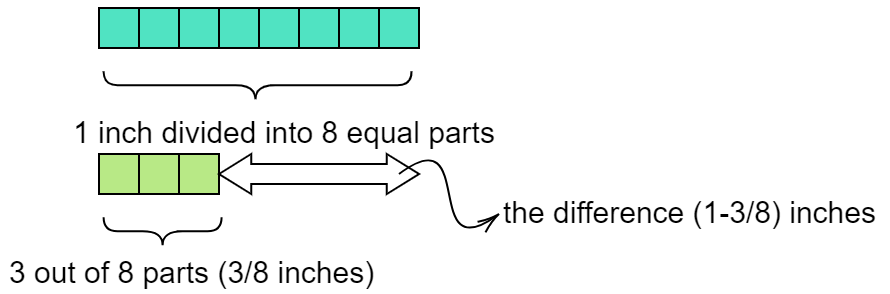
By comparing the quantities, we can say that $1 > \dfrac{3}{8}$
Since we must find how much is left of the first quantity after removing the second quantity, we shall write a subtraction equation.
$ \Rightarrow 1 - \dfrac{3}{8}$
We can write $1$ in fraction form as $\dfrac{1}{1}$,we can rewrite the equation as,
$ \Rightarrow \dfrac{1}{1} - \dfrac{3}{8}$
Now cross-multiply the fractions and then subtract the numerators and then multiply the denominators to get a common denominator.
$ \Rightarrow \dfrac{{(1 \times 8) - (3 \times 1)}}{{(1 \times 8)}}$
On further evaluation,
$ \Rightarrow \dfrac{{8 - 3}}{8}$
Which is equal to,
$ \Rightarrow \dfrac{5}{8}$

$\therefore $$1$ inch button is $\dfrac{5}{8}$ times longer than $\dfrac{3}{8}$ inch buttons.

Additional Information: Whenever there are different denominators in a subtraction equation, the first step must be to convert it in such a way to get the same denominators. Then only we should proceed to the subtraction operation. The quantity which is given in the question is an Inch which is a unit of length.$1$ inch$ = 2.54$ centimeters.
Note:
The above question can also be solved using LCM (least common multiples) method.
Firstly, write both the quantities in fraction form.
$ \Rightarrow \dfrac{1}{1};\dfrac{3}{8}$
Now, write the subtraction equation for the both quantities.
$ \Rightarrow \dfrac{1}{1} - \dfrac{3}{8}$
Now, find the multiples for the denominators
For $1$ the multiples are $1$,
For $8$ the multiples are $1\;,2,4,8,$
On comparing both the multiples, the LCM of $1$ and $8$ is $8$.
$\Rightarrow$$\dfrac{1}{1} = \dfrac{{(1 \times 8)}}{{(1 \times 8)}} = \dfrac{8}{8}$, (because $\dfrac{8}{1} = 8$)
$\Rightarrow$$\dfrac{3}{8} = \dfrac{{(3 \times 1)}}{{(8 \times 1)}} = \dfrac{3}{8}$, (because $\dfrac{8}{8} = 1$)
Therefore,
$ \Rightarrow \dfrac{8}{8} - \dfrac{3}{8}$
On further evaluation,
$ \Rightarrow \dfrac{5}{8}$