Question

Locate the center of mass of arrangement shown in figure. The three rods are identical in mass and length.

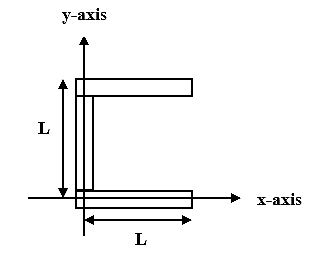
$A. \left(\dfrac {L}{2}, \dfrac {L}{2} \right)$
$B. \left (\dfrac {L}{3}, 0 \right)$
$C. \left( \dfrac {L}{3}, \dfrac {L}{2} \right)$
$D. \left (0, \dfrac {L}{2} \right)$

Answer 1

Hint: To solve this given problem, apply the concept of center of mass. So, first find the center of mass of each individual rod. Then, use the formula for X-coordinate of center of mass of the system. Substitute the values in the formula and find the X-coordinate of the center of mass of the system. Then, use the formula for Y-coordinate of center of mass of the system. Substitute the values in the formula and find the Y-coordinate of the center of mass of the system. This will give the center of mass of the arrangement.

Complete step-by-step solution:

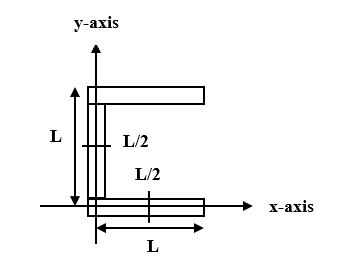
From the above figure, we can say, the center of mass of the rod along the X-axis is $\left (\dfrac {L}{2}, 0 \right)$.
$\therefore {x}_{1}= \dfrac {L}{2}, {y}_{1}=0$
Similarly, we can say, the center of mass of the rod along the Y-axis is $\left (0,\dfrac {L}{2} \right)$.
$\therefore {x}_{2}=0, {y}_{2}=\dfrac {L}{2} $
The center of mass of the remaining rod is
$ \left(\dfrac {L}{2}, L \right)$.
$\therefore {x}_{3}= \dfrac {L}{2}, {y}_{3}=L$
Let ${m}_{1}$, ${m}_{2}$ and ${m}_{3}$ be the mass of the rod along X-axis, Y-axis and the remaining rod.
It is given that the mass of each rod is the same.
$\therefore {m}_{1}={m}_{2}={m}_{3}=m$
We know, X-coordinate of center of mass of the system is given by,
${x}_{CM}= \dfrac { { m }_{ 1 }{ x }_{ 1 }+{ m }_{ 2 }{ x }_{ 2 }+{ m }_{ 3 }{ x }_{ 3 } }{ { m }_{ 1 }+{ m }_{ 2 }+{ m }_{ 3 } }$
Substituting values in above equation we get,
${x}_{CM}=\dfrac { \left( m\times \dfrac { L }{ 2 } \right) +\left( m\times 0 \right) +\left( m\times \dfrac { L }{ 2 } \right) }{ m+m+m }$
$\Rightarrow {x}_{CM}=\dfrac { \left( \dfrac { mL }{ 2 } \right) +0+\left( \dfrac { mL }{ 2 } \right) }{ 3m }$
$\Rightarrow {x}_{CM}= \dfrac { \left( \dfrac { 2mL }{ 2 } \right) }{ 3m }$
$\Rightarrow {x}_{CM}=\dfrac { mL }{ 3m }$
$\Rightarrow {x}_{CM}=\dfrac { L }{ 3 }$
Similarly. Y-coordinate of center of mass of the system is given by,
${y}_{CM}= \dfrac { { m }_{ 1 }{ y }_{ 1 }+{ m }_{ 2 }{ y }_{ 2 }+{ m }_{ 3 }{ y }_{ 3 } }{ { m }_{ 1 }+{ m }_{ 2 }+{ m }_{ 3 } }$
Substituting values in above equation we get,
${y}_{CM}=\dfrac { \left( m\times 0 \right) +\left( m\times \dfrac {L}{2} \right) +\left( m\times L \right) }{ m+m+m }$
$\Rightarrow {y}_{CM}=\dfrac {0+ \left( \dfrac { mL }{ 2 } \right) +\left( mL \right) }{ 3m}$
$\Rightarrow {y}_{CM}= \dfrac { \left( \dfrac { 3mL }{ 2 } \right) }{ 3m }$
$\Rightarrow {y}_{CM}=\dfrac { 3mL }{ 6m }$
$\Rightarrow {y}_{CM}=\dfrac { L }{ 2 }$
Thus, the center of mass of the arrangement is $\left( \dfrac {L}{3}, \dfrac {L}{2} \right)$.

So, the correct answer is option C i.e. $\left( \dfrac {L}{3}, \dfrac {L}{2} \right)$.

Note:
To solve these types of questions, students must have knowledge of the concept of center of mass. Or else they might make a mistake while calculating the center of mass of each individual rod. As it is given that the mass and length of the rods are equal, they should take this in consideration. Also, for simple rigid objects with uniform density, the center of mass is located at the centroid.