Question

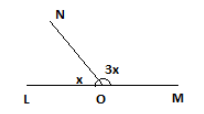
LM is a straight line and O is a point on LM. Line ON is drawn not coinciding with OL or ON. If \[\angle MON\] is three times \[\angle LON\], then \[\angle MON\] is equal to:
A) \[{45^ \circ }\]
B) \[{60^ \circ }\]
C) \[{105^ \circ }\]
D) \[{135^ \circ }\]

Answer 1

Hint: Total angle subtended by a straight line from a point is equal to \[{180^ \circ }\]. A straight line also known as a flat line is formed when the legs are pointing in exactly opposite directions where the vertex of the line measures \[{180^ \circ }\].
In this question it is mentioned that LM is a straight line where O is a midpoint and ON forms a line, since \[\angle MON\] is three times of \[\angle LON\], we know the total angles subtended by a straight line is \[{180^ \circ }\], so write the sum of \[\angle MON\] and \[\angle LON\] equal \[{180^ \circ }\].

Complete answer:
Given LM is a straight line with O being a point and \[\angle MON\], \[\angle LON\] being the angles on the straight line.
Let us consider, \[\angle LON = x\]
Since \[\angle MON\] is three times of \[\angle LON\], hence we can write
\[\angle MON = 3\left( {\angle LON} \right) = 3x - - - - (i)\]

                            

Since the total angle subtended by a straight line is\[{180^ \circ }\], hence we can write:
\[\angle LON + \angle MON = 180 - - - - (ii)\]
Substituting the value from equation (i) in equation (ii) as
\[
x + 3x = 180 \\
4x = 180 \\
x = \dfrac{{180}}{4} \\
= {45^ \circ } \\
\]
Hence the value of \[x = {45^ \circ }\]
Since, \[\angle LON = x\]
\[\therefore \angle LON = {45^ \circ }\]
Also, \[\angle MON = 3x\]
So the value of \[\angle MON = 3 \times 45 = {135^ \circ }\]
Hence \[\angle MON\] is equal to \[{135^ \circ }\].

Therefore the option (D) is correct.

Note: The different types of angles based on their measurements are acute angles, Right angles, Obtuse angle and straight angle. It is interesting to note here that, from the figure one can easily say that one of the angles is acute and the other one is obtuse and the same is our calculated answer.