Question

How many lines can pass through two given points?

Answer 1

Hint: Infinite number of lines can pass through a single point. Similarly, an infinite number of curves can pass through 2 points, which are not straight lines. Only 1 straight line can pass through 2 points.

Complete step-by-step answer:

Let us consider the 2 points as A and B.

Now, infinite lines can pass through the point A as shown below.

Similarly, infinite lines can pass through point B.

Now, Let's take two points A and B together will have one line passing through it.

Only through Point A \[\to \] Infinite lines.

Only through Point B \[\to \] Infinite lines.
Through A and B \[\to \] 1
Number of straight lines that can pass through 2 points A and B = 1.

Note:
Let us consider a case of non-collinear points. If we have been given 4 points and need to find how many lines can pass through these points.
The method is to find the number of straight lines that can be formed.

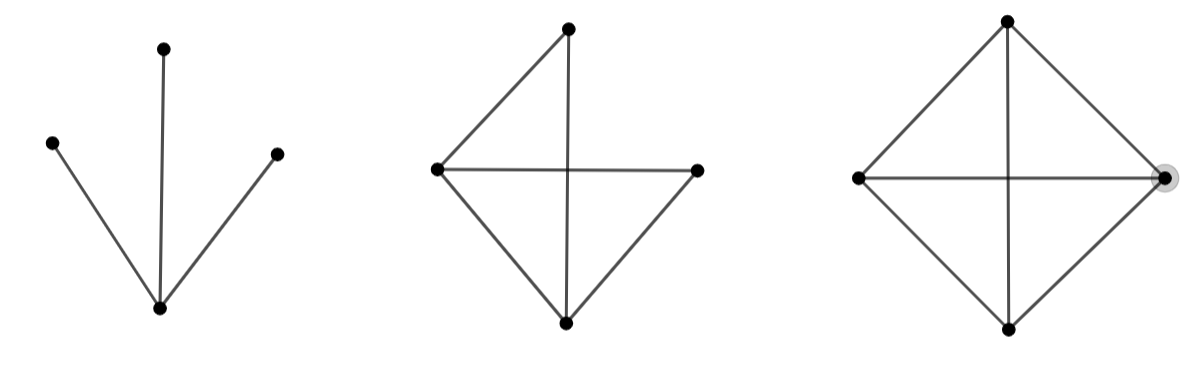
3 Lines 5 Lines 6 Lines
\[\therefore \](4 - 1) (4 - 1) + (4 - 2) (4 - 1) + (4 - 2) + (4 - 3) + (4 - 4)
\[\therefore \]They are of the form:
\[\begin{align}
  & h=\sum\limits_{i=1}^{n}{\left( n-i \right)}=\left( n-1 \right)+\left( n-2 \right)+\left( n-3 \right)+.....+\left( n-n \right) \\
 & =\sum\limits_{i=1}^{n}{n}-\sum\limits_{i=1}^{n}{i}\Rightarrow L={{n}^{2}}-\dfrac{n\left( n+1 \right)}{2}=\dfrac{2{{n}^{2}}-{{n}^{2}}-n}{2} \\
 & L=\dfrac{{{n}^{2}}-n}{2}=\dfrac{n\left( n-1 \right)}{2} \\
\end{align}\]
\[\therefore L=\dfrac{n\left( n-1 \right)}{2}\], where L = number of lines.
So, for 4 points, n=4,
\[L=\dfrac{4\left( 4-1 \right)}{2}=\dfrac{4\times 3}{2}=6\]lines.
Where n=1, \[L=\dfrac{1\left( 1-1 \right)}{2}=\dfrac{0}{2}\]i.e. Infinite number of lines.
Where n=2, \[L=\dfrac{2\left( 2-1 \right)}{2}=1\]etc.