Question

How many lines are determined from three distinct points?
(a)Two
(b)Three
(c)One or three
(d)Six

Answer 1

Hint: One line can be formed using the two coordinated on the plane i.e. for drawing a line, we need two points. So, draw three points on the sheet and try to observe how many lines can be formed with them by joining the points.

Complete step-by-step answer:

As we know any line is formed by joining two points on the plane. It means for one line two points are required.

Now, coming to the question, as we need to determine the number of lines that can be determined by three distinct points, we can use the fundamental concept of drawing one line i.e. two points are required for a while.

So, let us suppose three distinct point A, B and C as follow: -

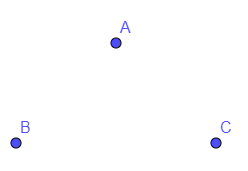
Now, let us try to draw a line with the help of joining two distinct points. So, we get that one line can be drawn by joining points A and B, another line can be formed by joining points B and C and similarly one more line can be drawn by joining points A and C. So, we can name the lines as AB, BC and AC. Hence, we get that only three lines are possible with the help of three distinct points.
So, option (b) is correct.

Note: Direct formula to get the number of lines by n points is $\dfrac{n\left( n-1 \right)}{2}$. So, one may use this formula as well. One may give an answer as 6, as he/she can consider line AB and BA, AC and CA, BC and CB as different line segments, which is wrong. They represent the same line (AB and BA). So, don’t confuse it with taking care for future reference.