Question

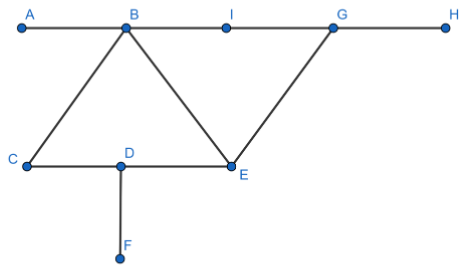
How many line segments are there in the given figure?

Answer 1

Hint: To calculate the total number of line segments, we need to follow the definition of line segment. The start to count the number of lines one by one lies within two points. Start counting the line segments from small line segments to big line segments that are in different directions and also choose the corresponding name.

Complete step by step solution:
Here, we will count all the horizontal line segments that lie within two nearest points as:
Line segment $AB$, line segment $BI$, line segment $IG$, line segment $GH$, line segment $CD$, line segment $DE$.
So, there are a total of $6$ small horizontal line segments.
Now, count that line segments that are joined by two small line segments.
Line segment $AI$, line segment $BG$, line segment $GH$ and line segment $CE$.
So, there are $4$line segments that are made by two line segments.
Now, Count that line segments that are made by three small line segments as:
Line segment $AG$ and line segment $BH$.
Here, we got $2$ line segments.
Thus, total horizontal line segments $=6+4+2=10$
Now, we will count the vertical line segment.
In the given diagram, there is only one vertical line segment available.
Thus, total vertical line segments $=1$
Now, count the diagonal vertical line segments.
Line segment $BC$, line segment $BE$ and line segment $EG$.
So, there are total $3$diagonal line segments.
Now, we will add all the types of line segments to calculate the total number of line segments.
Hence, Total number of line segments$=10+1+3=14$.

Note: Line segments are the line joint by two points and contain many different points in that line segment. In other words, line segments are lines with starting points and end points. And It contains many other points within the line segment.