Question

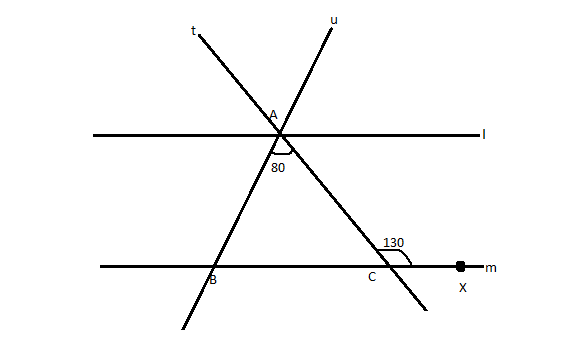
Line \[l\] is parallel to line \[m\] as shown in the above figure. Transversals \[t\] and \[u\] intersect at point \[A\] on \[l\] and intersect \[m\] at points \[C\] and \[B\], respectively. Point \[X\] lies on line \[m\], the measure of \[\angle ACX\] is \[130^\circ ,\] and the measure of \[\angle BAC\] is \[80^\circ \]. Find the number of angles formed by rays \[l,m,t,\] and \[u\] which have measure \[50^\circ .\]

A.4
B.6
C.8
D.10
E.12

Answer 1

Hint: Here, we have to find the number of angles formed by rays. We have to use the property of transversal lines and the property of triangles. A transversal line is a line that passes through two lines in the same plane at two distinct points.

Complete step-by-step answer:
We know that line \[l\] is parallel to line \[m\]and \[\angle ACX = 130^\circ \] and \[\angle BAC = 80^\circ \] .
In a triangle, exterior angle is equal to sum of interior opposite angles, we get
 \[ \Rightarrow \angle ACX = \angle ABC + \angle BAC = 130^\circ \]
 Substituting the angles, we have
\[ \Rightarrow \angle ABC + 80^\circ = 130^\circ \]

Rewriting the equation, we have
\[ \Rightarrow \angle ABC = 130^\circ - 80^\circ \]
\[ \Rightarrow \angle ABC = 50^\circ \]
Opposite angles are equal, we have
\[ \Rightarrow \angle ABC = \angle WBY = 50^\circ \]
 Sum of interior angles of a triangle are equal, we have
\[ \Rightarrow \angle BCA + \angle ABC + \angle BAC = 180^\circ \]
 Substituting the angles, we have
\[ \Rightarrow \angle BCA + 50^\circ + 80^\circ = 180^\circ \]
\[ \Rightarrow \angle BCA + 130^\circ = 180^\circ \]
 Rewriting the equation, we have
\[ \Rightarrow \angle BCA = 180^\circ - 130^\circ \]
\[ \Rightarrow \angle BCA = 50^\circ \]
 We know that the opposite angles are equal. Therefore, we get
\[ \Rightarrow \angle BCA = \angle XCZ = 50^\circ \]

We know that the alternate angles are equal. Therefore, we get
\[ \Rightarrow \angle SAC = \angle ACX = 130^\circ \]
Now, we have
\[ \Rightarrow \angle SAC = \angle SAB + \angle BAC\]
Substituting the angles, we have
\[ \Rightarrow 130^\circ = \angle SAB + 80^\circ \]
Rewriting the equation, we have
\[ \Rightarrow \angle SAB = 130^\circ - 80^\circ \]
\[ \Rightarrow \angle SAB = 50^\circ \]
Vertically Opposite angles are equal, we have
\[ \Rightarrow \angle SAB = \angle VAU = 50^\circ \]
Since \[t\] is a straight line, we have
\[ \Rightarrow \angle SAC + \angle SAT = \angle TAC = 180^\circ \]
Substituting the angles, we have
\[ \Rightarrow 130^\circ + \angle SAT = 180^\circ \]
 Rewriting the equation, we have
 \[ \Rightarrow \angle SAT = 180^\circ - 130^\circ \]
\[ \Rightarrow \angle SAT = 50^\circ \]
 We know that vertically opposite angles are equal, we get
\[ \Rightarrow \angle SAT = \angle UAC = 50^\circ \]
From the above calculation, we can conclude that
\[ \Rightarrow \angle ABC = \angle WBY = \angle BCA = \angle XCZ = \angle SAB = \angle VAU = \angle SAT = \angle UAC = 50^\circ \]
Therefore, the number of rays \[l,m,t,u\] which measures \[50^\circ \] is 8.

Note: For solving this question, we need to have knowledge about the properties of a Transversal line. When a transversal intersects two parallel lines then the corresponding angles are equal, then
1.The vertically opposite angles are equal.
2.The alternate interior angles are equal.
3.The alternate exterior angles are equal.
4.The pair of interior angles on the same side of the transversal is supplementary.
5.These properties would be helpful to find the angles.