Question

What is the limit of $\ln x$ as x approaches 0?

Answer 1

Hint: Assume the required limit as L. Now, to find the value of \[\displaystyle \lim_{x \to 0}\left( \ln x \right)\] we will check if the left hand limit, right hand limit and the value of the function at x = 0 exists or not. If they existed and are equal then that will be the answer. If any of the three values does not exist then the limit will be said to be non – existent. We will take the help of the graph of logarithmic function to get the conclusion.

Complete step by step answer:
Here we have been asked to find the limit of the logarithmic function as the domain value, i.e. x, tends to 0. Let us assume the limit value as L so mathematically we have,
$\Rightarrow L=\displaystyle \lim_{x \to 0}\left( \ln x \right)$
Now, we know that the value of limit of a function $f\left( x \right)$ exists at a point x = a only when we have the value of left hand limit, right hand limit and the value of the function at x = a exists, are equal and is a finite number. So mathematically we must have the condition:
$\Rightarrow \displaystyle \lim_{x \to {{a}^{-}}}f\left( x \right)=\displaystyle \lim_{x \to {{a}^{+}}}f\left( x \right)=f\left( a \right)$
Let us come to the question. Here we have $f\left( x \right)=\ln x$ and x = 0, so mathematically we must have the condition: $\displaystyle \lim_{x \to {{0}^{-}}}\left( \ln x \right)=\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln x \right)=\ln 0$ for the limit to exist. Let us check if the condition is satisfied by checking the graph of $\ln x$.

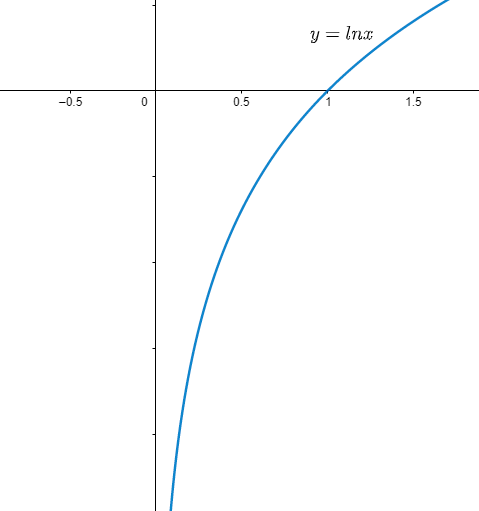
From the above graph it is clear that the logarithmic function is not defined for x < 0 and x = 0 therefore $\displaystyle \lim_{x \to {{0}^{-}}}\left( \ln x \right)$ and $\ln 0$ does not exist. Also we can see that as x tends to 0 from right the value of the function tends to $-\infty $ so $\displaystyle \lim_{x \to {{0}^{+}}}\left( \ln x \right)$ is not a finite number.
Hence, we can conclude that the limit does not exist.

Note: To solve the above question you must remember the graph of the logarithmic function and its domain values that makes the function defined. We can also understand the situation in a different manner by converting the log function into exponential function and drawing its graph. However, you must remember the basic requirement for the existence of the limit of a function.