Question

Like that image what is the rule for $\dfrac{d}{{dx}}(uv)$?

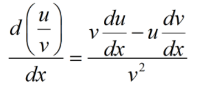
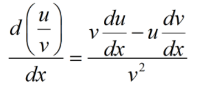
Answer 1

Hint:Let us assume u(x) and v(x) are two differentiable function of x and $f(x) = u(x)v(x)$ and then apply the definition of derivative of f(x),
$f'(x) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(x + h) - f(x)}}{h}$

Complete step by step answer:
As, $f(x) = u(x)v(x)$
Then, $f(x + h) = u(x + h)v(x + h)$
From the definition of derivative of f(x) we get, $
f'(x) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(x + h) - f(x)}}{h} \\
\Rightarrow f'(x) = \mathop {\lim }\limits_{h \to 0} \dfrac{{u(x + h)v(x + h) - u(x)v(x)}}{h} \\
\Rightarrow f'(x)= \mathop {\lim }\limits_{h \to 0} [\dfrac{{u(x + h)v(x + h) - u(x + h)v(x)}}{h} + \dfrac{{u(x + h)v(x) - u(x)v(x)}}{h}] \\
\Rightarrow f'(x)= \mathop {\lim }\limits_{h \to 0} [u(x + h)\dfrac{{v(x + h) - v(x)}}{h}] + \mathop {\lim }\limits_{h \to 0} [v(x)\dfrac{{u(x + h) - u(x)}}{h}] \\
\Rightarrow f'(x)= u(x)\mathop {\lim }\limits_{h \to 0} [\dfrac{{v(x + h) - v(x)}}{h}] + \mathop {v(x)\lim }\limits_{h \to 0} [\dfrac{{u(x + h) - u(x)}}{h}] \\
\therefore f'(x)= u(x)v'(x) + v(x)u'(x) \\
i.e.,\dfrac{d}{{dx}}[u(x)v(x)] = u\dfrac{{dv}}{{dx}} + v\dfrac{{du}}{{dx}} \\
$
Note:It is true for more than two differentiable functions. If a finite number of functions u, v, w, …….. are differentiable with respect to x, then
$\dfrac{d}{{dx}}(uvw...) = (vw...)\dfrac{{du}}{{dx}} + (uw...)\dfrac{{dv}}{{dx}} + (uv...)\dfrac{{dw}}{{dx}} + ...$